Hallo Mathelounge,
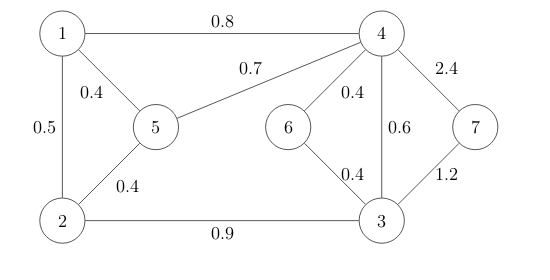
ich habe ein Beispiel zu einer Bestimmung des minimalen Spannbaumes nach dem Algorithmus von Kruskal.
Ist auch kein Problem, ein minimaler Spannbaum F wäre:
F = [{1,5} , {2,5} , {3,6} , {4,6} , {4,5} , {3,7}]
Meine Frage ist:
Dadurch, dass es 4 Kanten mit der gleichen geringsten Wichtung gibt, gibt es bei diesem Beispiel, von den Tupel her auch 24 verschieden Spannbäume, weil egal in welcher möglichen Reihenfolge man die ersten 4 Kanten wählt, bleibt der Rest gleich.
Das grafische Bild des minimalen Spannbaumes bleibt jedoch immer gleich.
Ist der minimale Spannbaum eindeutig, weil er immer gleich aussieht, oder ist er nicht eindeutig und es gibt 24 verschiedene minimale Spannbäume?
- Gast