Das Volumen einer quadratischen Pyramide wird mit der Formel:
$$ V = \frac{1}{3}·a^2 · h $$
Wir brauchen also die Höhe vom Mittelpunkt der Grundfläche bis zur Spitze. Diese Höhe ist die Kathete eines rechtwinkligen Dreiecks mit den Seiten
a = 1/2 d, b = h, c = Kantenlänge = a
d ist die Hypotenuse des Dreiecks mit den Katheten, die ebenfalls die Seitenlänge a haben, weil in einem Oktaeder die Seitenlängen der Grundfläche der Kantenlänge entsprechen.
d2 = a2 + a2
d2 = 2a2
$$ d = \sqrt{a·a^2} = a·\sqrt{2} $$
die Hälfte davon ist dann:
$$ \frac{a}{2} · \sqrt{2} $$
Wir haben also zur Berechnung der Höhe die Gleichung
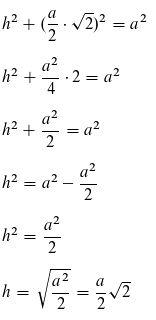
Das können wir für h in die Formel zur Berechnung des Volumens einsetzen:
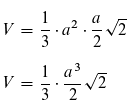
Da wir bei einem Oktaeder zwei dieser Pyramiden habenn, muss das Volumen noch mit 2 multipliziert werden. Die 2 im Zähler und 2 im Nenner werden gekürzt und damit bleibt
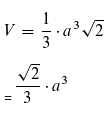
Oberfläche folgt...