Hi Lea,
das kriegen wir hin :-D
f(x) = 1/8 * x + 11/8 verläuft durch G und L.
f(x) hat welchen Anstieg?
Natürlich f'(x) = 1/8
Eine zu f(x) orthogonal verlaufende Funktion g(x) hat den negativ reziproken Anstieg von f(x), also Kehrwert bilden und mit -1 multiplizieren:
1/8 | Kehrwert = 8
8 * (-1) = -8 = g'(x)
Eine kleine Skizze dazu (g(x) und K konnte ich wegen des gegebenen Koordinatensystems nicht richtig einzeichnen):
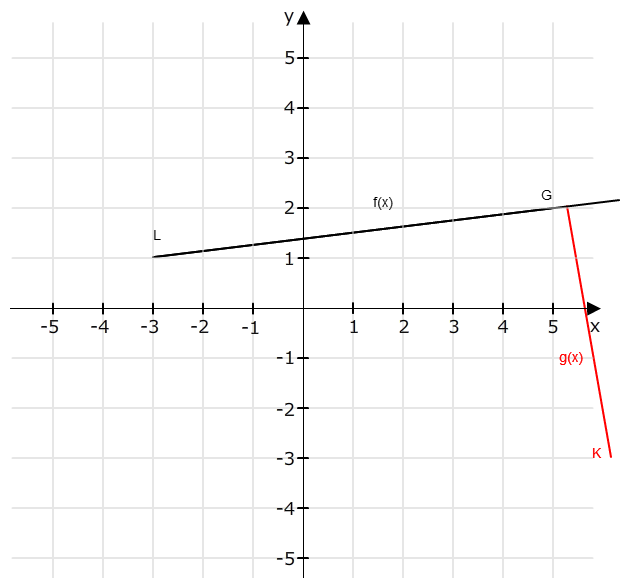
Jetzt können wir g(x) berechnen:
Wir wissen: g'(x) = -8
Und wir wissen auch, dass g(8) = -3
Also g(8) = -8 * 8 + c = -3
g(8) = -64 + c = -3
c = 61
g(x) = -8x + 61
Probe:
g'(x) = -8 | stimmt
g(8) = -8*8 + 61 = -64 + 61 = -3 | stimmt
Besten Gruß