Hallo DB,
dein Weg bei a) ist richtig.
b)
Der Graph geht durch die Punkte (0|48) , (4|400) , (8|960) und (12|1200)
das sind 4 Bedingungen. Damit ergibt sich ein Ansatz mit 4 Unbekannten:
f(x) = ax^3 + bx^2 + cx + d
f(0) = 48 → d = 48 → f(x) = ax^3 + bx^2 + cx + 48
f(4) = 400 → 64·a + 16·b + 4·c + 48 = 400
f(8) = 960 → 512·a + 64·b + 8·c + 48 = 960
f(12)=1200 → 1728·a + 144·b + 12·c + 48 = 1200
Lösen des LGS ergibt a = - 11/8 ∧ b = 23 ∧ c = 18
f(x) = -11/8 x^3 + 23 x^2 + 18x + 48
c)
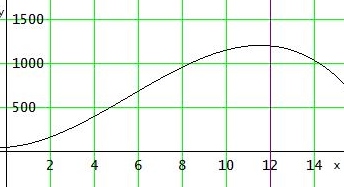
Die relativ starke Zunahme in den ersten Wochen spiegelt das Modell nicht wider.
d)
Hier musst du f "(x) = 46 - 33·x/4 = 0 setzen und erhältst x ≈ 5,6 [Wochen]
Zu diesem Zeitpunkt beträgt die momentane Gewichtszunahme
≈ f `(5,6) ≈ 146 [ g/Woche ]
Gruß Wolfgang