Ansatz fehlt - Tangente aus einem Punkt 0(0|0) auf den Graphen legen.

Question

Aufgabenstellung
Bestimmen Sie die Pukte P des Graphen g(x)= x^{2} - 4x + 9 so,
dass die Tangente in P durch den Ursprung geht. 

Unsicher.
Ich denke an Tangente an die Kurve legen,
wobei die Tangenten durch den Punkt O ( 0 | 0 ) gehen.

Frage / Problem
Ich weiss nicht wie ich am besten vorgehe und der "beiden" Berührungspunkte B den x und den y Wert festlege.

Gleichsetzen und nach der unbekannten Auflösen kann ich dann.

Answer 1

Hallo Limonade,

g(x)= x² - 4x + 9   ;  g '(x) = 2x -4

mit dem unbekannten Berührpunkt B( a | g(a) ) hat die Tangente die Gleichung

y = f'(a) * x   # 

B einsetzen:

a² - 4a + 9  = (2a - 4) * a      ⇔   9 - a² = 0   ⇔   a = ± 3

Berührstellen  a = ± 3  in  #  einsetzen:

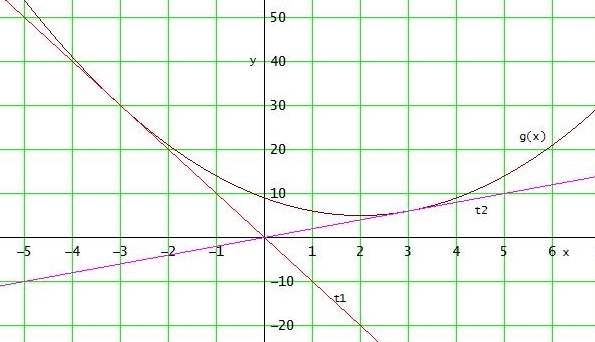
t₁:  y = - 10x        ;  t₂:   y = 2x

Gruß Wolfgang

Answer 2

Der Berührpunkt sei (u|v). Die Steigung an der Stelle u ist einerseits g'(u)=2u+4 und andererseits v/u. Daraus ergibt sich (1) v/u=2u-4. Außerdem ist (u|v) ein Punkt der Parabel, sodass gilt (2) v=u²-4u+9. Das sind zwei Gleichungen mit zwei Unbekannten.