Taschenrechner verwenden nur Näherungsformeln!
Wichtigste Randbedingung hast Du vergessen: Anzahl der benötigten Nachkommastellen, da es unendlich viele gibt!
Es gibt nun mehrere Algorithmen für ln(x):
a) Reihenentwicklung (unendliche Summe) für x nahe 2.
ln(x)=1 + (x - e)/e - (x - e)^2/(2 e^2) + (x - e)^3/(3 e^3) - (x - e)^4/(4 e^4) +...
ln(x)=1+sum ((-1)^{1 + n} e^{-n} (2-e)^n)/n ,n=1...∞
Für 4 richtige Nachkommastellen benötigt man mindestens 6 Summanden (min der 1 sind es 7) und e mit Genauigkeit von mindestens 2.718281828459...
ln(2)=1 + (2 - e)/e - (2 - e)^2/(2 e^2)+...- (2 - e)^6/(6* e^6)
=0.69316...
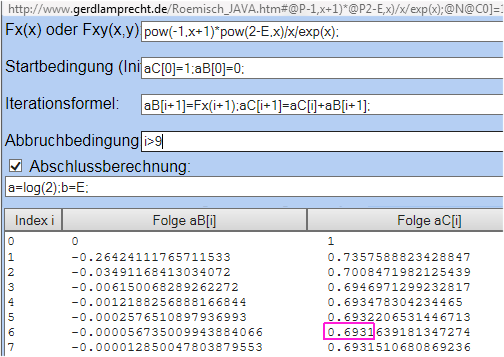
Da ich schlecht mit Papier & Bleistift bin, habe ich die einzelnen Summanden per Iterationsrecher in Spalte aB und die Summe bis dahin in Spalte aC abgelegt:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@P-1,x+1)*@P2-E,x)/x/exp(x);@N@C0]=1;@B0]=0;@N@Bi+1]=Fx(i+1);@Ci+1]=@Ci]+@Bi+1];@Ni%3E9@N0@N1@Na=log(2);b=E;
Dann gibt es noch:
b) fertige Tafeln (oft nur 3 richtige Stellen!)
https://images.booklooker.de/x/00WZgH/F-G-Gauss+F%C3%BCnfstellige-vollst%C3%A4ndige-Logarithmische-und-Trigonometrische-Tafeln-Zum-Gebrauche-f%C3%BCr.jpg
c) Rechenschieber:
http://www.hh.schule.de/metalltechnik-didaktik/museum/rechenschieber/tasche/26.jpg
d) Iterationen
... reicht für heute