Hallo Sara,
Wenn von einem 'gleichschenkligen Trapez' die Rede ist, so meint man ein Trapez, bei dem die beiden Seiten, die i.A. nicht parallel zu einander stehen, gleich lang sind (die Schenkel) und diese beiden Schenkel symmetrisch zueinander stehen!
Ein Trapez zeichnet sich dadurch aus, dass zwei gegenüberliegende Seiten parallel verlaufen, d.h. die haben überall den gleichen Abstand. Fällt man also das Lot von den Punkten \(C\) und \(D\) auf die Gerade durch \(AB\) und erhält dort die Fußpunkte \(F_c\) und \(F_d\), dann sind die Strecken \(CF_c\) und \(DF_d\) gleich lang.
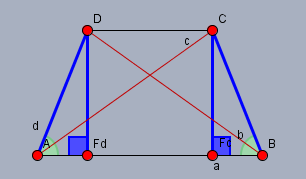
Nach dem vierten Kongruenzsatz SSW sind dann die beiden Dreiecke \(\triangle AF_dD\) und \(\triangle BCF_c\) kongruent (siehe die blau markierten Strecken und Winkel). Und somit sind auch die Winkel in \(A\) und \(B\) identisch (grün markiert). Mit dem zweiten Kongruenzsatz SWS lässt sich dann zeigen, dass \(\triangle ABD\) und \(\triangle ABC\) konkruent sind (SWS: \(DA, \space \angle BAD, \space AB\)) und (SWS: \(AB, \space \angle CBA, \space BC\)) (s. Wolfgangs Antwort).
Das oben gesagte gilt nicht, wenn die Schenkel nicht symmetrisch zueinander stehen, also der Winkel bei \(B\) in die andere Richtung zeigt:
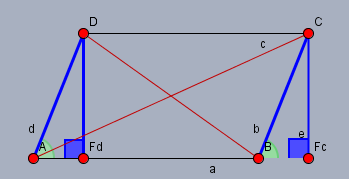
Ist einer der Winkel in einem gleichschenkligen Trapez =90°, so ist auch der Winkel am gleichen Schenkel und der gegenüberliegenden parallelen Seite =90° , da die Summe der beiden 180° ergeben muss (Winkel an Parallelen). Und da die Winkel an der gleichen parallelen Seite und dem anderen Schenkel ebenfalls gleich sind (wie oben gezeigt), sind alle Winkel =90° und demnach ist so ein Trapez ein Rechteck.
Gruß Werner