gleichschenkliges Trapez

Question

Wie konstruiere ich ein gleichschenkliges Trapez wenn ich weiß  dass zwei Seiten gleich lang (keine Weiteren Angaben) und ein Winkel ist gegeben (Spitzer Winkel ist gegeben den ich mit dem zirkel abtragen muss sonst darf ich nur mit den Zirkel arbeiten )

Answer 1

Hallo Anna-Lena,

ich nehme mal an, der Winkel ist in Form zweier Geraden \(g\) und \(h\) gegeben. Benenne den Scheitelpunkt mit \(A\).

 

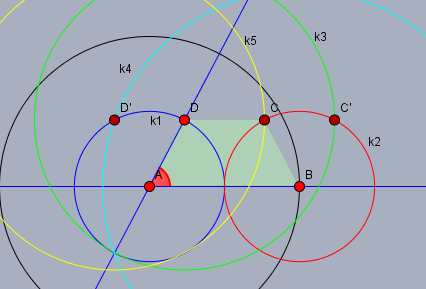
Ein Kreis (schwarz) mit Radius \(6\text{cm}\) um \(A\) schneidet \(g\) in \(B\). Der Kreis \(k1\) (blau) mit Radius \(3\text{cm}\) um \(A\) schneidet \(h\) in \(D\). Die Kreise \(k2\) (rot) mit Radius \(AD\) um \(B\) und \(k3\) (grün) mit Radius \(AB\) um \(D\) schneiden sich in \(C'\). Der Kreis \(k4\) (hellblau) um \(B\) mit Radius \(AC'\) schneidet \(k1\) in \(D'\). Der Kreis \(k5\) (gelb) mit Radius \(AB\) um \(D'\)  schneidet \(k2\) (rot) in \(C\). 

\(ABCD\) ist das gesuchte Trapez.

Answer 2

Offenbar geht es vor allem um das Konstruieren nur mit dem Zirkel. Hierzu haben der Italiener Mascheroni und der Däne Mohr sehr viel gesagt. In diesem Falle muss ein gegebener Winkel an einer selbstgewählten Achse gespiegelt werden, ohne dass diese Achse gezeichnet wird. Denn ein Lineal ist offensichtlich nicht erlaubt. Schlage einen Kreis K um den Scheitel S des gegebenen Winkels mit beliebigem Radius r. Der Kreis K schneidet die Schenkel g und h des gegebenen Winkels in A (auf g) und B (auf h). Wähle einen beliebigen Punkt P≠S auf g und schlage einen Kreis K₂ mit dem Radius r um P. K₂ schneidet g in C. Der Kreis um C mit dem Radius AB schneidet K₂ in D. SPDB ist ein gleichschenkliges Trapez.

Comments

Wie hat der Kreis um C den Radius von der Strecke AB muss der nicht kleiner sein? Und wieso brauche ich den Punkt C wenn er keinen Eckpunkt darstellt ? Kann ich nicht von P aus einen Kreis schlagen ? 

---

Die Aufgabe hat durch nachträgliche Kommentare ihren Charakter so sehr geändert, dass ich meine Antwort zurückziehe.

Answer 3

Falls sonst keine Angaben vorliegen dürfte
das Dreieck nicht zu konstruieren oder zu berechnen
sein. Eine Seitenlänge wäre von Vorteil.

Comments

Eine Seitenlänge wäre von Vorteil. 

b=7 cm.
Jetzt bin ich ja mal auf deine Konstruktion gespannt.

---

Die Strecke AB beträgt 6 cm und die seitenlängen b und c sind gleich lang mit je 3 cm  und ein Spitzer Winkel ist gegeben ( Alpha)