Desinfektion eines Erlebnisbades

Question

Durch Zugabe eines Desinfektionsmittels soll die Anzahl der Keime( in Mio. pro ml.) in einem Erlebnisbad verringert werden. Die danach vorhandene Keimanzahl wird nach Ansicht eines Experten beschrieben durch h (t)= 5+10e^-0,02t (t in Stunden). Ein zweiter Experte vertritt die Meinung, dass die Funktion g(t)=15-0,12t die Anzahl der Keime zutreffend angibt.

a) Welche Anzahl von Keimen enthält 1 ml Wasser in beiden Modellen 10 Stunden nach der Desinfektion?

b) Wann ist in beiden Modellen die Keimzahl auf die Hälfte des Anfangsstandes gefallen?

c) Für welchen Zeitpunkt ist der Unterschied beider Prognosen am größten?

Answer 1

Hallo Janet,

a) Welche Anzahl von Keimen enthält 1 ml Wasser in beiden Modellen 10 Stunden nach der Desinfektion?

wenn du  t=10 in beide Funktionsgleichungen einsetzt, erhältst deu

h(10)  ≈ 13.19   ;    g(10)  =  13,8

b) Wann ist in beiden Modellen die Keimzahl auf die Hälfte des Anfangsstandes gefallen?

Der Anfangswert beträgt in beiden Modellen  h(0) = g(0) = 15, die Hälfte ist also  7,5
5 + 10e^-0,02t = 7,5   →    t₁ = 69.31   [Stunden]  
15 - 0,12t = 7,5  →   t₂ = 62.5   [Stunden] 

c) Für welchen Zeitpunkt ist der Unterschied beider Prognosen am größten?

Der  Unterschied beider Prognosen  ist  u(t)  = | d(t) |  =  | f(t) - g(t) | 
d(x) = 5 + 10·e^{- 0.02·t} - (15 - 0.12·t)
u(x) = | 5 + 10·e^{- 0.02·t} - (15 - 0.12·t) 

Wenn man u(x) plottet:

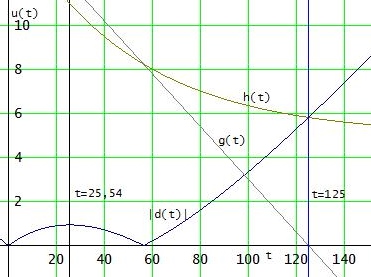
erkennt man ein lokales Maximum bei  t ≈ 25,54
Diesen t-Wert erhält man, wenn man d'(x) = 0 setzt:
d'(x) = 3/25 - 1/5 ·e^{- t/50} = 0
Das ist aber kein absolutes Maximum des Unterschieds, denn u(x) ist zum Beispiel bei x=80 größer und hat dann bei der Nullstelle  t = 125 von g(t) das absolute Maximum,                    weil für t > 125  g(t) negativ ist und keinen Sinn mehr macht.

Gruß Wolfgang