Hallo Kristin,
kommt darauf an, ob Du es zeichnerisch oder rechnerisch lösen sollst. Rechnerisch berechne zu jedem Punkt die Differenz zu \(Z\), multipliziere diese mit dem Streckungsfaktor \(2,5\) und addiere das Ergebnis wieder auf \(Z\). Somit ergeben sich die drei Bildpunkte
$$A'=2,5 \cdot \left( \begin{pmatrix}2\\ 0\end{pmatrix} - \begin{pmatrix}-1\\ 0\end{pmatrix} \right) + \begin{pmatrix}-1\\ 0\end{pmatrix} = \begin{pmatrix}6,5\\ 0\end{pmatrix}$$
$$B'= 2,5 \cdot \left( \begin{pmatrix}4\\ 0\end{pmatrix}- \begin{pmatrix}-1\\ 0\end{pmatrix}\right) + \begin{pmatrix}-1\\ 0\end{pmatrix} = \begin{pmatrix}11,5\\ 0\end{pmatrix}$$
$$C'= 2,5 \cdot \left( \begin{pmatrix}2\\ 3\end{pmatrix}- \begin{pmatrix}-1\\ 0\end{pmatrix}\right) + \begin{pmatrix}-1\\ 0\end{pmatrix} = \begin{pmatrix}6,5\\ 7,5\end{pmatrix}$$
Zeichnerisch beginne mit dem Dreieck wie es angegeben ist und zeichne den Punkt \(Z\) ein. Dann ziehe durch jeden der drei Punkte und durch \(Z\) einen Strahl (gelb). In diesem Fall deckt sich der Strahl durch \(A\) mit dem durch \(B\). Anschließend zeichne einen dritten Strahl (grün), auf dem Du ausgehend von \(Z\) fünfmal die gleiche Streck abträgst. Vom zweiten Punkt \(1\) bis zum fünften \(2,5\) hast Du dann das Längenverhältnis \(2\div 5 = 1 \div 2,5\).
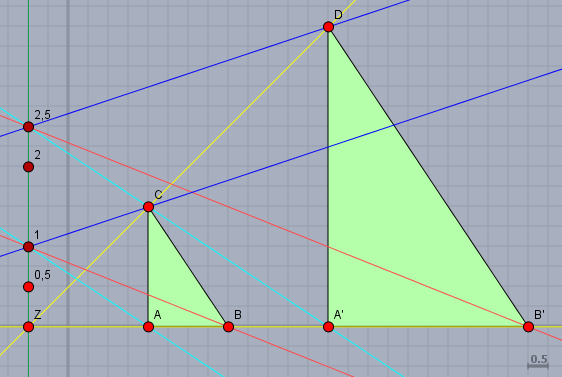
Jetzt verbinde jeden der drei Punkt \(A\), \(B\) und \(C\) mit dem Punkt \(1\) (die hellblaue, rote und blaue Gerade) und zeichen zu jeder der drei Geraden eine Parallele durch den Punkt \(2,5\). Diese Parallelen schneiden dann die gelben Strahlen in den neuen Punkten \(A'\), \(B'\) und \(C'\) des gestreckten Dreiecks.