Vollständige Induktion

Question

Wie beweise ich das? kann mir jemand alle Schritte zeigen und ausführlich darlegen.

Beweisen Sie mit vollständiger Induktion:

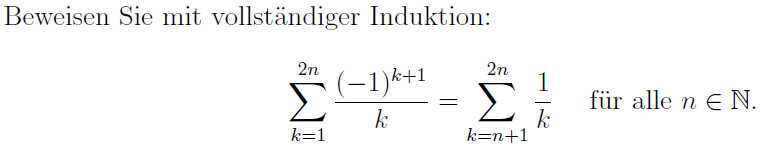
$$\sum _ { k = 1 } ^ { 2 n } \frac { ( - 1 ) ^ { k + 1 } } { k } = \sum _ { k = n + 1 } ^ { 2 n } \frac { 1 } { k } \quad \text { für alle } n \in \mathbb{N}$$

Comments

Ausfuehrlich dargelegte Beispiele zur vollstaendigen Induktion mit allen Schritten gibt es wie Sand am Meer im Netz (z.B. in diesem Forum) und in Lehrbuechern. Wozu brauchst Du noch ein weiteres Beispiel? Was versprichst Du Dir davon?

Answer 1

Induktionsvoraussetzung sei erledigt. Addiere jeweils den nächsten Summanden der Reihe. Das ist links (-1)²ⁿ⁺²/(2n+1) und rechts 1/(2n+1). Diese beiden Summanden sind gleich. Da nach Voraussetzung auch die Reihen ohne den letzten Summanden gleich sind, ist der Schritt von n auf n+1 gelungen.

Comments

Dir scheint ja leider überhaupt nicht klar zu sein, dass die linke Summe doppelt so viele Summanden hat wie die rechte.