Man könnte das ganze auch programmiertechnisch angehen, wie es in der Skizze angedeutet wird und darauf aufbauend eine Summe mit belibiger Obergrenze a*n-1 nehmen:
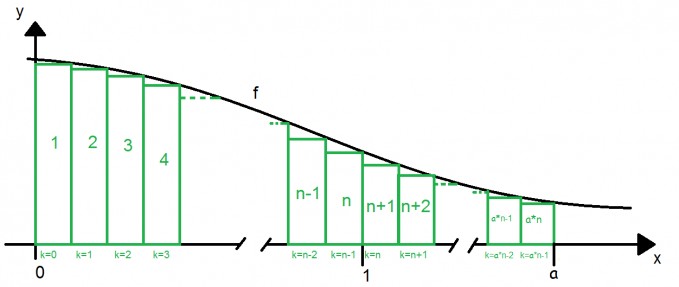
$$ A_k=\frac{1}{n}\cdot f(x),\text{ mit } x:=\frac{k}{n} $$Dann hätte man $$ \sum_{k=0}^{a\cdot n-1}{A_k}=\sum_{k=0}^{a\cdot n-1}{\frac{1}{n}\cdot f\Bigg(\frac{k}{n}\Bigg)}=\frac{1}{n}\cdot\sum_{k=0}^{a\cdot n-1}{ f\Bigg(\frac{k}{n}\Bigg)} $$
Übertragen auf beide Funktionen hätte man also folgende Näherungsresultate:
$$ g(x)=(1+x)^3\quad :\int_{1}^{3}{\sqrt{1+9(1+x)^4}}dx\\\stackrel{n=1000}{\approx} \frac{1}{1000}\cdot\Bigg[ \Bigg(\sum_{k=0}^{3\cdot 1000-1}{\sqrt{1+9\Big(1+\frac{k}{1000}\Big)^4}}\Bigg)-\Bigg(\sum_{k=0}^{1\cdot 1000-1}{\sqrt{1+9\Big(1+\frac{k}{1000}\Big)^4}}\Bigg)\Bigg]\\\approx63,102-7,078=56,024$$
$$ f(x)=sin(x) \quad :\int_{0}^{\frac{\pi}{2}}{\sqrt{1+cos^2(x)}dx}\\\stackrel{n=10000}{\approx}\frac{1}{10000}\cdot\sum_{k=0}^{\frac{3,141}{2}\cdot10000-1}{\sqrt{1+cos^2\Big(\frac{k}{10000}\Big)}}\approx 1,909$$
Bei pi/2 muss man hier allerdings ,,schummeln'', was aber für große n widerum keine bedeutende Rolle mehr spielen würde.
Python-Code:
from math import*
n = int(input(' n = ')) #Einteilungsschritte
a = float(input(' a = ')) #Obergrenze
summe = 0
k=0 #Laufvariable k
while k<=a*n-1: #Es wird solange aufaddiert, bis diese Bedingung nicht mehr gilt
summe = summe+sqrt(1+cos(k/n)**2)
k = k+1
print(summe/n)