Hallo Max,
Die Aufgabe ist Mist! Versuche mal das Dreieck \(\triangle ABM\) zu zeichnen. Die längste Seite \(MB\) ist genauso lang wie die Summe der beiden anderen Seiten \(MA\) und \(AB\). D.h. das Dreieck ist 'entartet'; die drei Punkte \(A\), \(B\) und \(M\) liegen auf einer Geraden! Ist das aus einem Schulbuch?
Aber nehmen wir mal an, \(\triangle ABM\) wäre ein 'normales' Dreieck:
Ist meine A richtig wie kann ich das hier begründen
Du kannst es über den Ähnlichkeitssatz begründen: Zwei Dreiecke sind ähnlich, wenn sie in zwei Winkeln übereinstimmen.
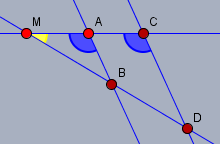
Der gelbe Winkel ist für beide Dreiecke der selbe und die blauen sind Stufenwinkel an Parallelen. Beide Dreiecke haben also zwei (und damit auch drei) identische Winkel und sind somit ähnlich.
Was soll ich bei der b ändern
Dein Ansatz \(MA \div MC = MB \div MD\) ist richtig. \(MD=7,5\text{cm}\) ist auch richtig. Den Rest der Rechnung für \(MC\) ist nicht sichtbar. Roland hat es Dir schon aufgeschrieben:
$$MC = \frac{MA \cdot MD}{MB} = \frac{MA \cdot (MB + BD)}{MB} = MA + \frac{BD}{MB} = 4,6875 \text{cm}$$
Bei der Berechnung von \(CD\) hast Du den falschen Ansatz gewählt \(MA \div AB \ne MD \div CD\). Richtig wäre
$$\frac{M\colorbox{#ffff00}{B}}{AB} = \frac{MD}{CD} \quad \text{oder} \quad \frac{MA}{AB}=\frac{M\colorbox{#ffff00}{C}}{CD}$$ wobei die erste Variante vorzuziehen ist, da sie nicht vom (evt. falschen!) Zwischenergebnis \(MC\) abhängt. $$\Rightarrow CD = \frac{AB\cdot MD}{MB} = 2,8125 \text{cm}$$
Zur Kontrolle: Die Summe \(MC+CD\) muss wieder \(MD=7,5\text{cm}\) ergeben, da \(\triangle CDM\) genauso entartet ist, da es ja zu \(\triangle ABM\) ähnlich ist.
Gruß Werner