Winkel berechnen in dreidimensionaler Konstruktion

Question

Ich möchte in der angefügten dreidimensionalen Konstruktion den gekennzeichneten Winkel α berechnen. Dabei ist der Winkel β= 30°, δ= 5° und ε= 8° bekannt. Zudem sind die Winkel ∠ABD, ∠ACB, ∠ACE und ∠EFB jeweils 90°.

Das ganze kann ich im CAD-System modellieren und die Winkel herausmessen. So wäre in diesem Fall der gesuchte Winkel α 30.94778°. Interessiert bin ich jedoch an der Gleichung für α.

Folgendes habe ich bereits notiert:
a=sin(α)*c
b=cos(α)*c
c=cos(δ)*e
d=\( \sqrt{b^2+n^2} \)
e=1
h=a−sin(ε)*n
m=sin(δ)*d = \( \sqrt{e^2-(cos(δ)*e)^2} \)
n=\( \frac{m}{cos(ε)} \)

Mit Hilfe des Kosinussatzes lässt sich ebenfalls sagen:
h2=e2+d2−2⋅e⋅d⋅cos(β)
Dadurch sollten für h zwei Gleichungen bekannt sein, welche man nun gleichsetzen kann. Allerdings scheitere ich beim Auflösen.

I) h=a−sin(ε)*n=sin(α)*cos(δ)*1−sin(ε)*(sin(δ)*d/cos(ε))
II) h^2=e^2+d^2−2*e*d* cos(β)

Kann mir hier jemand helfen? Oder hat jemand einen anderen Ansatz?
Falls die Konstruktion unklar sein sollte, gerne einfach nachfragen.

Comments

Hat sich erledigt, da sich bei der Vereinfachung der Aufgabe ein Fehler eingeschlichen hat...

---

Vom Duplikat:

Titel: Winkel berechnen in komplexer, dreidimensionaler Geometrie

Stichworte: 3d,geometrie,winkel,kosinussatz,sinussatz

Aufgabe:

In der dargestellten Geometrie sind neben den markierten rechten Winkeln die Winkel β, δ und ε bekannt. Die Geraden m und l sind zudem parallel.

Daraus soll nun der Winkel α bestimmt werden.

Problem/Ansatz:

Die Geometrie habe ich im CAD modelliert und kann den geforderten Winkel messen. Interessant ist jedoch die Formel, mit welcher α direkt berechnet werden kann.

Einen wirklichen Lösungsansatz habe ich bisher noch nicht, daher bin ich um jede Unterstützung dankbar.

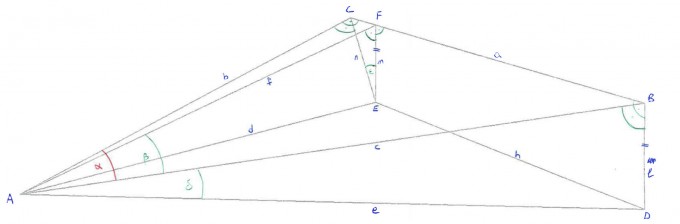
Als Hilfe bzw. zur Überprüfung kann ich ein Zahlenbeispiel aus dem CAD-Modell geben.

β = 30°

δ = 10°

ε = 20°

a (CB) = 54.73605

b = 83.6897

c = 100

d = 84.79089

e = 101.54266

f = 83.81926

l = 17.6327

m = 12.79951

n = 13.62095

α = 33.186117°