Konvergenz - Wie ist der Ausdruck bzw. die Distanz |an-a|<epsilon geometrisch auf dem Zahlenstrahl zu interpretieren ?

Question

Definition. 
$$ \begin{array} { l } { \text { Zu jedem } \varepsilon > 0 \text { existiert ein } N \in \mathbb { N } , \text { so dass } } \\ { \left| a _ { n } - a \right| < \varepsilon \text { für alle } n \geqslant N . } \end{array} $$

Problem.

Ich widme mich dem Ausduck 

| a_n - a |

etwas genauer, weil ich den etwas besser Verstehen will. 


Also:
Damit ist der Absolutbetrag gemeint. 
Also kommt die Fallunterscheidung zum Zuge. 

1. Fall, positiv
+(a_n-a) , falls an-a ≥ 0
 = a_n-a

2. Fall, negativ
-(an-a) , falls an-a < 0 
= -an + a
= a - an

Frage:

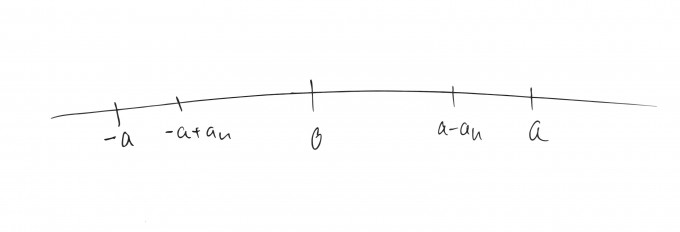
Wenn ich mir diese Umgebung auf einem Zahlenstrahl aufzeichnen will, zeichne ich den Punkt a zunächst auf dem horizontalen Zahlenstrahl ein, dann gehe ich gemäss Fall zwei etwas weiter Links und zeichne a-an ein. Danach soll die Umgebung wieder zurück bom Punkt a aus gesehen noch um etwa den gleichen Betrag nach rechts gehen, dies tut es nicht, denn die neue Umgebung geht gemäss Fall 1 von einem Punkt -a aus und addiert den Abstand an von dort aus nach rechts. 


Bild:

Answer 1

 | a - a_n |  ist der Abstand auf dem Zahlenstrahl zwischen a und a_n .