Vektorgeometrie Verschiebung berechnen

Question

Guten Tag Zusammen

Kann mir hier jemand helfen?

Aufgabe: Ein Dreieck ist aus dem Punkt A(2/11.75) ausgehend durch die Seitenvektoren

aufgespannt.

a) Bestimmen Sie eine Parametergleichung der Schwerlinie durch den Punkt A.

(2/11.75)+t(-4/13)

b) Um wie viel muss das Dreieck in y-Richtung verschoben werden, bis die Schwerelinie, bzw. deren Verlängerung, durch den Punkt P(-6/-4) geht.

Lösen Sie die Aufgabe rechnerisch mit Hilfe der Vektorgeometrie.

Wie geht Aufgabe b)?

Ich habe versucht b mit dieser Formel zu berechnen:

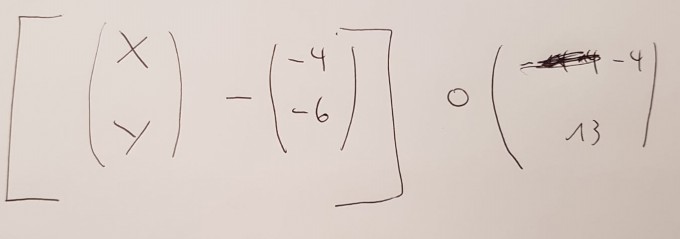
bin jedoch auf t=-691/740 gekommen laut den Lösungen sollte ich auf t=-2 kommen. Was mache ich falsch?

LG
AP2019

Answer 1

Hallo

wenn du das Dreieck in y Richtung verschiebst, wird aus der y-Komponente von A 11,75+y das y suchst du so dass

(2|11,75+y)+t*(-4|13)=(-4|-6) ist, dabei ist nach y nicht nach t gefragt, t bestimmt sich schon aus der x Komponente.

Gruß lul

Answer 2

a) Bestimmen Sie eine Parametergleichung der Schwerlinie durch den Punkt A.

1/2·([3.5, 16.75] + [-11.5, 9.25]) = [-4, 13]

g: X = [2, 11.75] + r·[-4, 13]

b) Um wie viel muss das Dreieck in y-Richtung verschoben werden, bis die Schwerelinie, bzw. deren Verlängerung, durch den Punkt P(-6 | -4) geht.

X = [2, 11.75] + r·[-4, 13] + [0, y] = [-6, -4] → y = -41.75 ∧ r = 2
Die Gerade muss um 41.75 in negative y-Richtung verschoben werden.