Konstruiere ein Viereck Lösungsidee , Lösungsweg

Question

Konstruiere ein Viereck Lösungidee + KB Danke

Comments

KB=?

Was für ein Viereck soll es denn sein? Allgemein? Ein Rechteck? Ein Trapez?

---

KB bedeutet vermutlich Konstruktionsbeschreibung. Das hilft aber auch nicht weiter ...

---

Ich hoffe, dass Sie das Bild jetzt sehen können. Danke

---

Hallo Teresa, 

eine sehr schwierige Aufgabe.

Man zeichnet zuerst die Diagonale e ein, die durch A und C begrenzt wird. Dann schlägt man um C einen Kreis mit dem Radius c = 9,7 cm und um A einen Kreis mit dem Radius d = 7,2 cm. 

Die beiden Kreise schneiden sich in zwei Punkten; man nimmt den linken Schnittpunkt und erhält so D. 

Wir erhalten in etwa folgendes Dreieck (passt nicht genau, weil ich am PC keinen Zirkel verwenden kann):

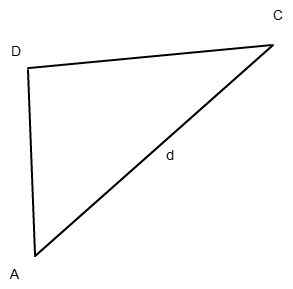
(Die Strecke heißt natürlich nicht d, sondern e.)

 

Nun dachte ich, dass der angegebene Winkel der untere Innenwinkel sei, was aber wohl nicht stimmt :-(

 

Ich habe irgendwo auf e diesen Winkel von 82° angelegt und dann eine Parallele zu dieser Geraden durch D gezogen: 

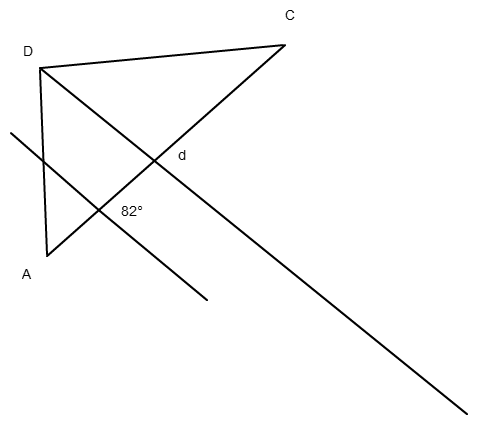
Dann wollte ich um A einen Kreis mit dem Radius 5,1 cm schlagen und den Schnittpunkt mit der Diagonale f als B erhalten; dazu ist der Kreis aber zu klein. 

Momentan sehe ich auch keine Lösung. 

(Die anderen habe ich Thomas übrigens an seine E-Mail-Adresse geschickt.)

 

Lieben Gruß

Andreas

Answer 1

Hallo Teresa, 

was lange währt, wird endlich gut :-)

Hier siehst Du das Ergebnis:

Ich habe zuerst die Diagonale e eingezeichnet, eine Strecke von 12,3 cm, und so A und C erhalten.

Dann habe ich einen Kreis mit Radius 9,7 cm um C geschlagen und einen weiteren Kreis um A mit Radius 7,2 cm. Der linke Schnittpunkt dieser beiden Kreise lieferte den Punkt D.

Den Winkel von 82° habe ich mit der grünen Hilfslinie abgetragen; eine Parallele dazu wurde durch den Punkt D gezogen, so dass ich die zweite Diagonale des Vierecks (von D nach B) erhielt.

Auf dieser Diagonalen musste B liegen, aber auch 5,1 cm von A entfernt. Also habe ich einen Kreis mit Radius 5,1 cm um A geschlagen, und der rechte Schnittpunkt mit der Diagonalen lieferte schließlich den Punkt B.

 

Liebe Grüße

Andreas