Question

wie kriege ich für 0=x^3+3x^2-4 die Nullstellen raus?

Answer 1

Hi,

Rate!^^

x^3+3x^2-4 = 0

x = 1 ist eine Nullstelle, was man leicht durch probieren rausfindet. Damit dann eine Polynomdivision machen:

(x^3+3x^2-4)/(x-1) = x^2+4x+4 = (x+2)^2

Die weiteren Nullstellen sind also x_2,3 = -2

 

Grüße

Answer 2

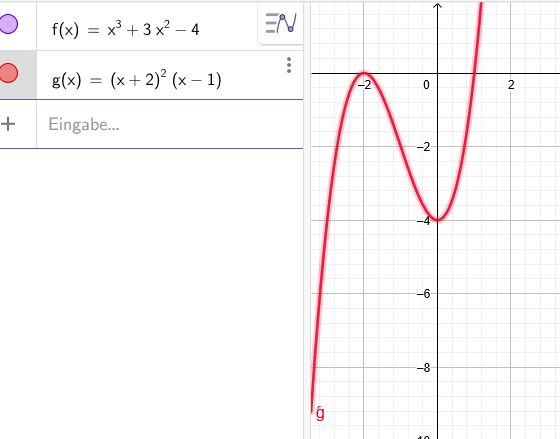
\(f(x)=x^3+3x^2-4\)

\(f´(x)=3x^2+6x\)   →   \(3x^2+6x=0\)→  \(x^2+2x=0\)

\(x_1=0\)   \(f(0)=-4\) Tiefpunkt

\(x_2=-2\)  \(f(-2)=0\) Hochpunkt als doppelte Nullstelle

\(x^3+3x^2-4=(x+2)^2*(x-N)=x^3+4x^2-Nx^2+4x-4Nx-4N\)

\(x^3+3x^2-4=x^3+x^2*(4-N)+x*(4-4N)-4N\)

Koeffizientenvergleich:

1.)

\(4-N)=3\) → \(N=1\)

2.)

\(4-4N=0  \)→ \(N=1\)

3.)

\(-4N=-4  \)→ \(N=1\)

\(f(x)=x^3+3x^2-4=(x+2)^2*(x-1)\)

Polynomdivision ist auch noch ein gangbarer Weg:

(x^3+3x^2-4):(x+2)^2=(x^3+3x^2-4):(x^2+4x+4)=...