Aufgabe:
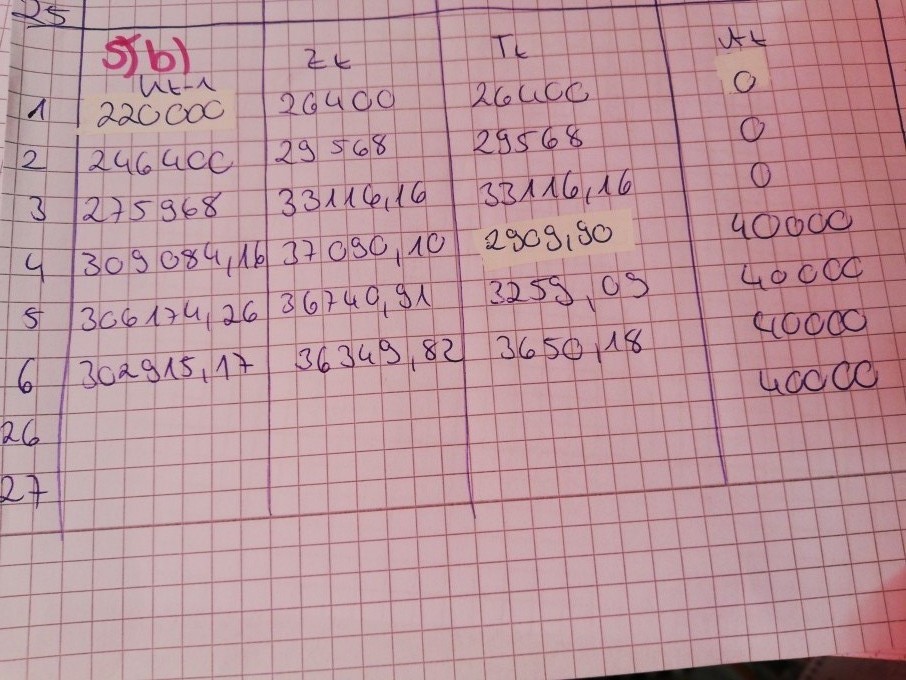
Ein Unternehmen nimmt einen Kredit über 220000€ auf. Die erste Rückzahlung (Annuität) erfolgt nach 4 Jahren iHv 40000€. Vorher leistete das Unternehmen keinerlei Zahlungen! Der Unternehmer zahlt seinen Kredit weiterhin mit jährlich gleichbleibender Annuität iHv 40000€ pro Jahr zurück. Die bank fordert Zinsen von 12% p.a..
a) nach welcher Zeit - bezogen auf den Tag der Kreditaufnahme - ist die Schuld vollständig bezahlt?
b) stellen sie für die ersten 6 und die letzten beiden Jahre einen Tilgungsplan auf
c) wie ändert sich die Laufzeit, wenn das Unternehmen in den ersten 3 Jahren jeweils am Jahresende die anfallenden Zinsen zahlt und danach(erstmalig am Ende des vierten Jahres) mit konstanten Annuitäten von je 40000€ pro Jahr den Kredit zurückzahlt
Das Problem ist, dass die ersten 4 Jahre nicht gezahlt wird und dadurch meine Formeln nicht funktionieren
a) meine ursprüngliche Formel funktioniert hier nicht, n=Log(A/T1)/Log(1+p)
n soll 27 sein
Welche muss ich denn nehmen?
b) wie berechne ich den Wert für das 26. Jahr? Da funktioniert meine Formel Kt=K0*((1+p)^n-(1+p)^t)/((1+p)^n-1)
c) welche Formel nehme ich da? Ich kann ja nicht den ganzen Tilgungsplan wieder aufstellen und ablesen, oder doch?
Prbordert /Ansatz: