Parameter Bestimmung einer Gerade

Question

Ich soll den Parameter der Geradengleichung so bestimmen, dass die Gerade den Graphen von f berührt und ich soll die Koordinaten des Berührpunktes bestimmen.

f(x) = 4x² + 3x + 2

g(x) = -3x + c

ein Parameter ist ja ein Unbekannter soweit ich weiß in einer Geradenglei. m und b

aber wie soll ich ihn bestimmen wenn er schon gegeben ist, dann müsste ich ja eig. nur den Berührpunkt ausrechnen mit der Formel b² - 4ac oder?

sehe ich das falsch, oder gibt es einen anderen Lösungsweg?

Answer 1

Wenn die Gerade g den Graphen von f berühren soll, muss die Differenz

d(x) = f(x)-g(x) eine doppelte Nullstelle haben.

d(x) = 4x²+3x+2+3x-c = 4x²+6x+2-c

d(x) = 0 ⇔ 4x²+6x+2-c = 0

x_1/2 = -3/4±√(1+4c)/4.

x₁ = x₂ ⇔ 1+4c = 0 ⇔ c = -1/4.

Also ist für c = -1/4 B(-3/4|f(-3/4)) Berührpunkt.

Answer 2

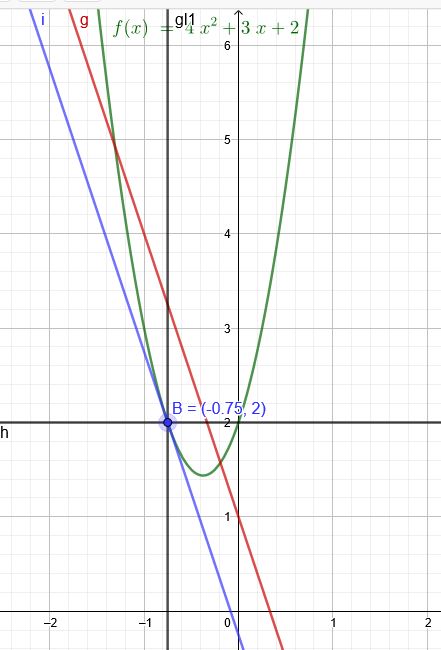
\(f(x) = 4x^2+ 3x + 2\)       \(g(x) = -3x+c\)

\( 4x^2+ 3x + 2=-3x+c\)     

\( 4x^2+ 6x =c-2\)   

\( x^2+ 1,5x =\frac{c-2}{4}\) 

\( x^2+ 1,5x+(\frac{1,5}{2})^2 =\frac{c-2}{4}+(\frac{1,5}{2})^2\)

\( (x+\red{0,75})^2 =\frac{c-2}{4}+(0,75)^2\)

Der Berührpunkt liegt nun an der Stelle \(x=-0,75\)

\(f(-0,75)=2\)

c berechnen:

\( \sqrt{\frac{c-2}{4}+(0,75)^2}=0\)

\(c=-\frac{1}{4}\)

Tangente:

\(t(x) = -3x-\frac{1}{4}\)