Du zeichnest zunächst ein Koordinatensystem. Meist zeigt die Y-Achse horizontal nach rechts, die Z-Achse vertikal nach oben und die X-Achse im Winkel von 45° nach links unten. Ansonsten kannst Du das Koordinatensystem zeichnen wie Du möchtest, aber das wäre eine übliche Art und Weise.
Du solltest die Achsen noch bemaßen. Bei der horizontalen und vertikalen Achse kannst Du Dich an den Kästchen auf dem Papier orientieren. Bei der schrägen Achse wählt man oft die Hälfte des Einheitsquadrats als den Wert 1.
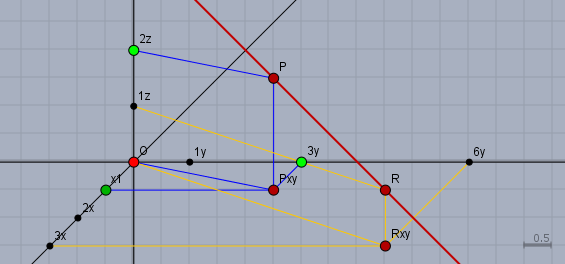
Du solltest zunächst lernen, wie man einen einzelnen Punkt mit festen Koordinaten einzeichnet. Hier z.B.: $$P = \begin{pmatrix} 1\\ 3\\ 2 \end{pmatrix}$$Dazu markierst Du auf jeder der drei Achsen, die Koordinaten - also bei \(x=1\), \(y=3\) und \(z=2\) - das sind die grünen Punkte. Dann wählst Du eine Ebene - z.B. die XY-Ebene - und zeichnest durch die x- und y-Koordinate eine Parallele zur jeweils anderen Achse, die sich hier in \(P_{xy}\) schneiden. Das ist schon die Projektion des Punktes \(P\) in die xy-Ebene. Anschließend zeichnest Du eine Parallele zur dritte - also der Z-Achse und eine Paralle zur Verbindungsgeraden vom Ursprung \(O\) und \(P_{xy}\). Die beiden Parallelen schneiden sich in \(P\).
Für die Gerade benötigst Du noch einen zweiten Punkt \(R\) auf derselben. Addiere einfach \(P\) mit dem Richtungsvektor. Du kannst jedes Vielfache des Richtungsvektors benutzen, je nach dem wo Du den Punkt gut zeichnen kannst. $$R = P + \begin{pmatrix} 2 \\ 3\\ -1\end{pmatrix} = \begin{pmatrix} 3 \\ 6\\ 1\end{pmatrix}$$Seine Koordinaten sind die kleinen schwarzen Punkte. Jetzt in der gleichen Weise den Punkt \(R\) konstruieren und anschließend ist die gesuchte Gerade, die rote, die durch \(P\) und \(R\) verläuft.
siehe auch dieser Beitrag bei onlinemathe.de.
Gruß Werner