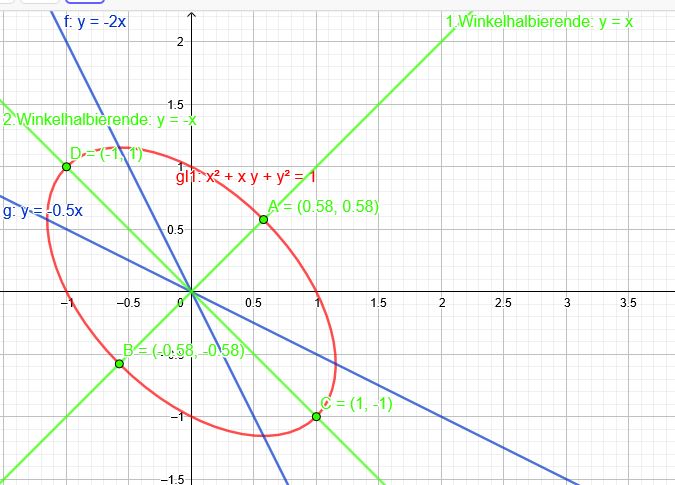
Welche Punkte der durch die Gleichung \(x^2 +y^2 +xy = 1\) gegebenen Ellipse mit Mittelpunkt \(M(0|0)\) haben vom Koordinatenursprung extremalen Abstand?
\(f(x,y)=x^2 +y^2 +xy -1\)
\(f_x(x,y)=2x+y\) → \(2x+y=0\) → \(y=-2x\) \(m_1=-2\)
\(f_y(x,y)=2y+x\) → \(2y+x=0\) → \(y=-0,5x\) \(m_2=-0,5\)
Die Winkelhalbierende der Geraden \(y=-2x\) und \(y=-0,5x\) schneiden die Ellipse in 2 extremalen Punkten
Steigung der 1.Winkelhalbierenden ist \(m_1\cdot m_2=1 \)
\(y=x\) schneidet \(x^2 +y^2 +xy =1\) in \(x^2 +x^2 +x^2=1\) →
→\(x_1=\frac{1}{3}\sqrt{3}\) \(y_1=\frac{1}{3}\sqrt{3}\) Koordinate \(A(\frac{1}{3}\sqrt{3}|\frac{1}{3}\sqrt{3})\)
→\(x_2=-\frac{1}{3}\sqrt{3}\) \(y_2=-\frac{1}{3}\sqrt{3}\) Koordinate \(B(-\frac{1}{3}\sqrt{3}|-\frac{1}{3}\sqrt{3})\)
Abstand zum zum Mittelpunkt \(d_1=\sqrt{(\frac{1}{3}\sqrt{3})^2+(\frac{1}{3}\sqrt{3})^2} =\sqrt{\frac{2}{3}}≈0,82\)
Die orthogonale Winkelhalbierende (2.) hat die Gleichung \(y=-x\)
\(y=-x\) schneidet \(x^2 +x^2 -x^2 =1\) in \(x^2=1\) →
→\(x_1=1\) \(y_1=-1\) Koordinate \(C(1|-1)\)
→\(x_2=-1\) \(y_2=1\) Koordinate \(D(-1|1)\)
Abstand zum zum Mittelpunkt \(d_2=\sqrt{1^2+1^2} =\sqrt{2}≈1,41\)
Minimaler Abstand zum Mittelpunkt ist \(d_1≈0,82\)
Maximaler Abstand zum Mittelpunkt ist \(d_2≈1,41\)