Hallo. Wie löse ich diese Aufgabe?
Aufgabe 4 (Die Tortenstückmethode). Man kann aus der Formel für den Um- fang U eines Kreises vom Radius r eine Formel für den Flächeninhalt A herleiten (oder umgekehrt), indem man eine Beziehung zwischen den beiden Größen her- stellt, ohne diese Formeln zu verwenden. Dies ist das Ziel dieser Aufgabe.
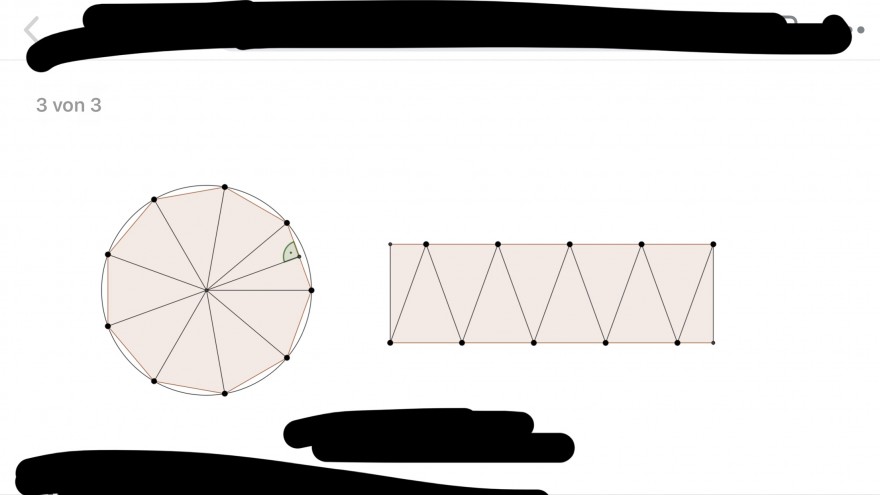
In einen Kreis vom Radius r wird ein regelmäßiges n-Eck einbeschrieben. Hierbei ist n ∈ N (und n ≥ 3). Unten ist der Fall n = 9 gezeichnet. Verbindet man die Eckpunkte mit dem Mittelpunkt des Kreises, entstehen auf diese Weise n kongru- ente Dreiecke, deren Höhe wir mit hn bezeichnen. Den Umfang des entstehenden n-Ecks bezeichnen wir mit Un, den Flächeninhalt mit An.
a) Aus der geometrischen Situation wird plausibel, dass die Folgen (hn), (Un) und (An) jeweils einen Grenzwert besitzen — welchen? (Die Angabe der Grenzwerte genügt.)
b) Man kann die eingezeichneten Dreiecke nebeneinander zu einem Rechteck auslegen, wenn man eines der Dreiecke noch halbiert (und gegebenenfalls eine Hälfte spiegelt). Unten ist der Fall n = 9 gezeichnet. Welcher Zusam- menhang ergibt sich damit zwischen hn, Un und An? Erläutern Sie in ein bis zwei Sätzen. (Warum haben die rot eingezeichneten Strecken an den eingezeichneten Punkten eigentlich keine Knicke?)
c) WelcheBeziehungergibtsichausdenobigenInformationen(ohneVerwen- dung von Formeln für Flächeninhalt bzw. Umfang) zwischen dem Umfang und dem Flächeninhalt des Kreises?
Text erkannt:
3 von 3
$$ N $$