Aufgabe:
Betrachten Sie erneut die Situation des Gasverbrauchs einer Kleinstadt vom letzten Übungsblatt:
\( \begin{array}{l|lllllll}{\text { Zeitpunkt }} & {1} & {2} & {3} & {4} & {5} & {6} & {7} \\ \hline \text { Gasverbrauch } & {18} & {17} & {9} & {27} & {20} & {18} & {8} \\ {\text { Temperatur }} & {10} & {6} & {14} & {-1} & {5} & {8} & {11}\end{array} \)
Das Regressionsmodell zur Erklärung des Gasverbrauchs in Abhängigkeit von der Tagestemperatur wurde geschätzt mit \( \hat{\beta}_{0}=25.95 \) und \( \hat{\beta}_{1}=-1.22 . \) Dies führt zu:
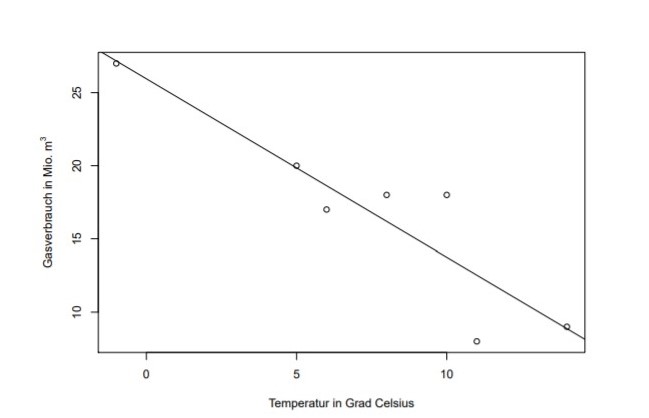
Text erkannt:
1
a) Bestimmen Sie die Residuen des Modells und erstellen Sie einen Residualplot.
kann mir jemand vielleicht erklären, wie man die Residuen berechnet? Hab schon etwas gegooglet, aber nichts hilfreiches gefunden.