Tangenten Abstand berechnen

Question

Hallo ich brauche Hilfe

Gegeben ist die Funktion f(x) =1/3x³-1/2x²-2x

Ableitung von der Funktion ist

f(x) =x²-x-2

Welchen Abstand haben die Tangenten?

Danke

Comments

Welche Tangenten?

---

Ahso

t2(x) =4x+10/3

t1(x) =4x+13,5

---

Die Gerade y=\(- \frac{1}{4} x\) steht senkrecht auf beiden Tangenten.

Berechne einfach die Schnittpunkte von  y=\(- \frac{1}{4} x\) mit beiden Tangenten.

Der Abstand der Schnittpunkte entspricht dem Abstand der Tangenten.

Answer 1

~plot~ 1/3*x^3-1/2*x^2-2x;x^2-x-2;4x+10/3;4x+13.5 ~plot~

Den Abstand der Tangenten könnte man leicht bestimmen. Ich frage mich aber ob das mit den "Tangenten" so seine Richtigkeit hat. Du weißt was eine Tangente ist?

d = (13.5 - 10/3)/√(4^2 + 1^2) = 61/102·√17 = 2.466

Comments

Ich habe die Punkten des graphen mit Steigung 4 gefunden. Ahso die Punkte sind P1(3|-1,5) und P2(-2|-2/3)

---

Das ist soweit richtig. Dann solltest du nochmals die Tangenten bestimmen.

---

Dann ich habe die Tangenten Gleichung

---

Nur für dich zur Kontrolle. Der richtige Abstand der Tangenten sollte dann vermutlich 5.053 sein.

---

Hey, wie berechnet man den Abstand der Tangenten? Das hab ich nicht verstanden also wie bist du auf 5.053 gekommen?

---

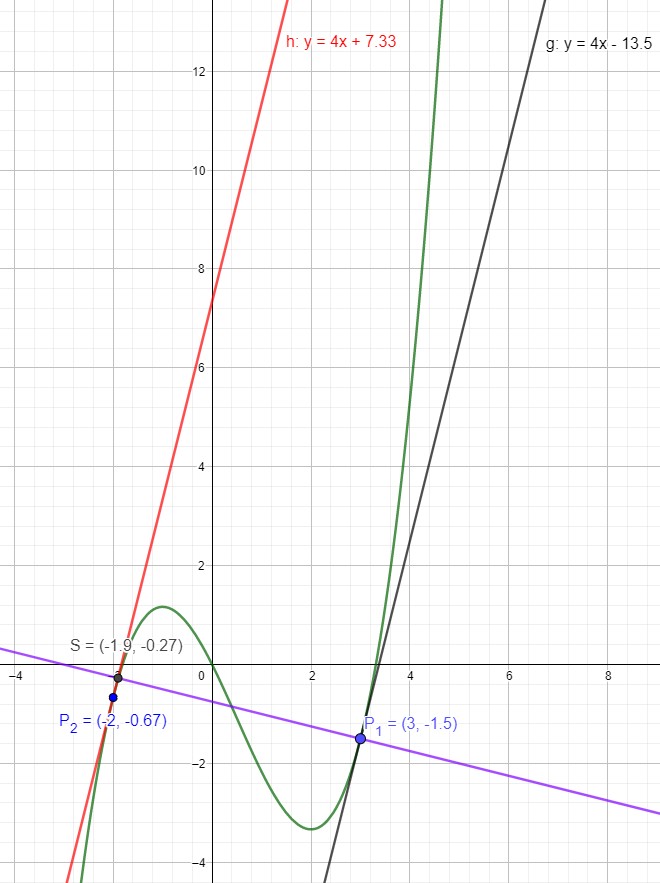
Das kannst du so berechnen:

Wähle den Punkt P1 auf g und stelle die Gleichung der Lotgeraden auf, die senkrecht durch diesen Punkt verläuft. l(x) = mx + n

m = -0,25 (negativer Kehrwert der Steigung von g)

Um n zu bestimmen, setze die Koordinaten von P1 in die Gleichung ein:

\(-1,5=-\frac{1}{4}\cdot 3+n\\n=-\frac{3}{4}\\l(x)=-\frac{1}{4}x-\frac{3}{4}\)

Berechne die Koordinaten des Schnittpunktes von l(x) und h(x):

\(-\frac{1}{4}x-\frac{3}{4}=4x+\frac{22}{3}\Rightarrow S(-1,9|-0,27)\)

Setze die Koordinaten von S und P1 in die Abstandformel ein.

\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\=\sqrt{(3+\frac{97}{51})^2+(-1,5+\frac{14}{51})^2}=5,0528255\approx5,053\)