Prisma schwierige Aufgabe

Question

5. Berechne das Volumen des Balkens B, wenn seine Querschnittsfläche ein Quadrat mit der Seitenlänge \( 12 \mathrm{cm} \) ist.

Problem/Ansatz:

es ist eine Bonusaufgabe. Deshalb ist sie so knifflig. Ich hoffe jemand von euch kommt draus....

Comments

Tipp: Pythagoras, Strahlensatz, ähnliche Dreiecke, Sinus und Co.

Answer 1

Zunächst mal muss man davon ausgehen das der Winkel der rechtwinklig aussieht auch tatsächlich rechtwinklig ist. Ansonsten wäre die Aufgabe nicht lösbar.

Ich würde es dann so rechnen:

d = √(280^2 + 120^2) = 40·√58

V = 1/2·(280·120 - (280 - 12·40·√58/120)·(120 - 12·40·√58/280))·12 = 41481 cm³

Skizze

Hier darfst du erkennen, dass die erkennbaren Dreiecke alle ähnlich sind.

Comments

Vielen Dank. Dürfte ich noch fragen, weshalb sie einmal durch 280 teilen und einmal durch 120?

---

Alle Dreiecke sind ähnlich. Das hilft die Seitenlängen in den kleinen Dreiecken zu bestimmen.

---

Gut, das Wort "ähnlich" hast du inzwischen selbst erkannt.

Bitte bearbeit mal noch die missverständliche Zeile, die mit

A=   beginnt und mit Kubikzentimetern endet.

---

Ok. Habe das A durch V ersetzt.

Answer 2

Der abgebildete Balken geht noch "12 cm nach hinten".

Bestimme also die abgebildete Fläche und multipliziere sie mit 12 cm.

Da es sich um eine Bonusaufgabe handelt, halte ich es für verwerflich, dir die Aufgabe fertig vorzurechnen.

Hier liegt keine Notsituation vor.

Mach was draus.

Comments

Also 2.8*1.2*12?

Answer 3

Dreieck OAB, OA=1.2, OB=2.8

Wenn wir das eine Ende gucken

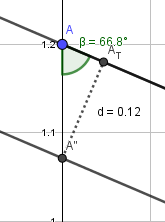
Berechne die Hypotenuse AA'' ==> OA''

Und am anderen Ende (Eckpunkt B) analog...===> B'' ==> OB''

Dann hast die Maße für das große Dreieck OAB und für das keine Dreieck OA''B'' unter dem Balken, Mit der Tiefe des Balkens bilden sie je ein Dreicksprisma. z.B.

V_OAB = 1.2*2.8*0.12/2

V_OA''B'' =

Comments

Vielen Dank für die Lösung , doch keider verstehe ich sie nicht. Ich kann die Hypotenuse doch gar nicht austechene, da ich keine rechten Winkel habe. Könntest du vielleicht deinen Rechenweg aufschreiben. Ich wäre sehr dankbar dafür.

---

Also ich sehe in der Abbildung sehr wohl einen rechten Winkel bei A_T.

Nochmal: Für Bonuspunkte sollte man auch selbst eine Bonusleistung erbringen.

---

Die Zeit bzw. Abgabe war schon längst. Das bedeutet ich bekomme so oder so keine Punkte. Aber ich möchte auch nicht unbedingt die Punkte, sondern ich möchte die Aufgabe verstehen und in Moment verstehe ich sie nicht. Deshalb schreibe ich meine Frage auch hier hinein damit mir jemand helfen kann. Und mir würde es am meisten helfen, wenn jemand mir den Rechenweg mit den Zahlen aufzeigt, denn so kann ich es am besten nachvollziehen. Ich bin eben so ein Lerntyp.

---

Eigentlich ist hier nicht markiert, dass der Winkel rechtwinklig ist. Man müsste es aber annehmen, da man sonst ein Freiheitsgrad hat und die Aufgabe nicht eindeutig lösbar ist.

---

Genau das meine ich @Der_Mathecoach. Könnten sie mir vielleicht helfen?

Wäre sehr dankbar

---

Du hast meine Rechnung ja bereits gesehen.

---

@Goli

Ein größerer Maßstab

Der Winkel β ist berechenbar über die Katheden OA, OB gegeben

β=arctan(2.8 / 1.2)

Bei A_T ist sehr wohl ein ⊥ ==> sin(β)=d/AA''

usw.

Analog die Ecke B

---

Der Winkel β ist berechenbar ..

ich vermute, dass Goli noch keine Trigonometrie hatte. Ist hier auch nicht nötig - siehe Antwort vom Mathecoach.