Steigung Steigungsdreieck

Question

Hallo Leute

In einer Aufgabe stand man muss die Steigung im Punkt P(2|f(2)) bestimmen.

Es war nur ein Schaubild leider ohne Funktion.

Der Punkt P(2|f(2)) war kurz vor dem Hochpunkt, hatte positive x und y Koordinate. Man kann sich die Funktion so wie f(x)=-x²+6 vorstellen.

In Musterlösung haben die den Steigungsdreieck sehr komisch gelegt, die haben schon auf der y-Achste angefangen und nach rechts gegangen und dann nach oben.. warum haben die das so gemacht? Ich hätte gleich im f(2) angefangen nach rechts zu gehen und dann nach oben..

Vielen Dank

Comments

Kannst du ein Bild der Lösung posten?

Answer 1

Steigung im Punkt P(2|f(2))

y = -x^2+6

Nun müsste ich schon sehen, was die gemacht haben.

Grundsätzlich gilt: Je grösser ein Steigungsdreieck, desto genauer kannst du im Graphen eine Steigung (Höherndifferenz und Horizontaldistanz) ablesen. Voraussetzung, die Hypotenuse verläuft im fraglichen Punkt echt parallel zur Kurve.

Hast du ein x vergessen?

Ich könnte mir anhand deiner Beschreibung ungefähr Folgendes vorstellen:

Plotlux öffnen

f₁(x) = -x²+6xx = 2f₂(x) = 8Zoom: x(-1…7) y(-1…10)f₃(x) = 1,7x+4,6

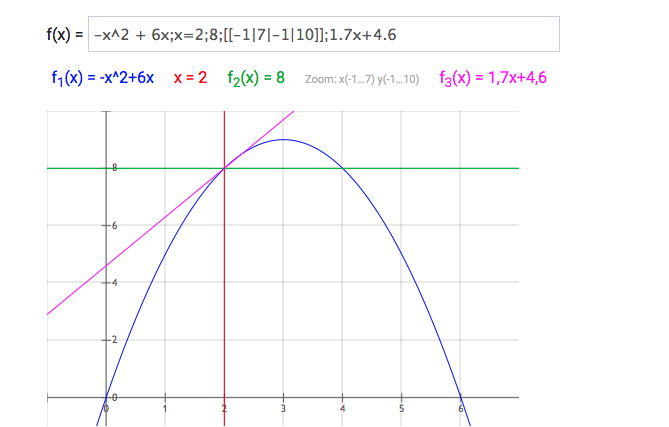
Text erkannt:

$f(x)=-x^{\wedge} 2+6 x ; x=2 ; 8 ;[[-1|7|-1 | 10]] ; 1.7 x+4.6$
$f_{1}(x)=-x^{\wedge} 2+6 x \quad x=2 \quad f_{2}(x)=8 \quad$ Zoom: $x(-1,7) y(-1,10) \quad f_{3}(x)=1,7 x+4,6$
3

Comments

Hey ja genauso sah es aus, der Punkt war kurz vor Höhepunkt und die Tangente genauso eingezeichntet. Die im Musterlösung haben schon in der y-Achse angefangen mit den Steigungsdreieck also von Schnitt der Tangente mit y-Achse nach rechts und dann nach oben..

ich hätte gleich von Punkt P nach rechts gegangen und dann nach oben..

---

Ok. Wie gesagt: Grösser bedeutet meist genauer. Du siehst auch besser, ob die Tangente wirklich parallel zur Kurve verläuft, wenn du sie nicht allzu knausrig einzeichnest. Allzu ungenau wird dein Resultat aber wohl nicht sein.