Bakterien Wachstum berechnen

Question

Aufgabe: Salmonellen wurden bei 37 Grad C in einem geeigneten Nährmedium und Laborbedingungen kultiviert und die optische Dichte (Trübung des Nährmediums) alle 10 min gemessen.

Es wurde gefunden, dass die Verdopplungszeit der Bakterien etwa 30 min beträgt.

Problem/Ansatz:

Ich soll die Zeit Berechnen ab dem ein ''Kartoffelsalat'' nicht mehr essbar wäre durch den oben genannten text. Ich soll davon ausgehen, dass sich das Wachstum in der log-phase befindet.

log-phase=  Exponentielles Wachstum der Bakterien durch anpassung ihres SToffwechsels an ihre Umgebung

Answer 1

Wie viel Salmonellen befinden sich am Anfang im Salat und ab wie viel Salmonellen ist der Salat ungenießbar?

Es ist verständlich das du eine Aufgabe nicht lösen kannst, wenn du nicht mal alle wichtigen Daten dem Text entnehmen kannst.

Comments

Tut mir leid, mein Fehler.

Ist die Verdopplungszeit bekannt, so kann die Wachstumsrate durch Einsetzen in die Exponential Funktion und Umstellen nach r bestimmt werden. Ist die Wachstumsrate bekannt, kann die Bakterienzahl für einen beliebigen Zeitpunkt t bestimmt werden.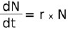

r= Zuwachsrate

N= Populationsgröße

trägt man die Anzahl der Individuen N gegen die Zeit t auf, so ist die änderung der Individuenzahl dN mit der Zeit dt (1. ABleitung) abhängig von der Wachstumsrate r und der Individuenzahl N.

Mehr hab ich leider auch nicht, bin am verzweifeln wegen der Aufgabe, das sind alle mir gegebenen infos.

Text erkannt:

\( \frac{d N}{d t}=r \times N \)

Answer 2

N(t) = N(0)*2^(t/30)

N(0)= Anfangsbestand

N(t)= kritischerBestand

t in Minuten