Wie weit ist das Schiff vom Leuchtturm entfernt?

Question

Aufgabe:

13) Ein Schiff fährt in östlicher Richtung. Den Leuchtturm „Felsencliff“ sieht man unter dem Winkel von 30° von der Nordrichtung nach Osten abweichend.
10 Seemeilen weiter sieht man vom Schiff den Leuchtturm unter dem Winkel von 10° von der Nordrichtung nach Osten abweichend. Wie weit ist das Schiff vom Leuchtturm entfernt?

Answer 1

Hallo,

eine schöne Navigationsaufgabe ;-) das nennt man eine Versegelungspeilung.

Das beginnt immer mit einer Skizze:

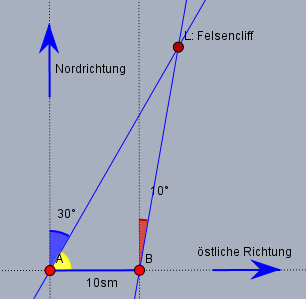
Das Schiff bewegt sich von der Position \(A\) nach Postion \(B\). Der Leuchtturm \(L\) bleibt natürlich immer an der gleichen Stelle. Da sich das Schiff bewegt, sieht man den Leuchtturm aber - je nach Postion - unter verschiedenene Winkeln. Einmal unter \(30°\) (blauer Winkel) und einmal unter \(10°\) (roter Winkel) beides bezogen auf die Nordrichtung.

Die Punkte \(A\), \(B\) und \(L\) bilden ein Dreieck, von dem zwei Winkel (bei \(A\) und \(B\)) und eine Strecke \(|AB|=10 \text{sm}\) bekannt sind. Gesucht ist der Abstand der aktuellen Schiffsposition \(B\) vom Leuchtturm \(L\) - also die Strecke \(|BL|\).

Ist Dir der Sinussatz bekannt?

Zur Kontrolle: \(|BL| = 25,3 \text{sm}\).

Gruß Werner