Aufgabe:
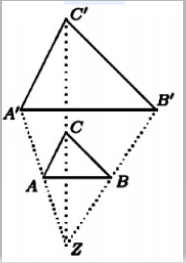
Bei zentrischen Streckungen gibt es ein Streckungszentrum \( Z, \) von dem aus eine Figur (z. B. das Dreieck \( \Delta A B C \) ) zur Bildfigur \( \left(\Delta A^{\prime} B^{\prime} C^{\prime}\right) \) gestreckt wird. \( Z \) liegt auf den Geraden Punkt-Bildpunkt \( \left(\text { also } A A^{\prime}, B B^{\prime}, C C^{\prime}\right) \)
(a) Drúcke den Streckungsfaktor \( m \) auf verschiedene Weisen aus.
(b) Es gibt auch zentrische Streckungen mit \( m<0 . A \) und \( A^{\prime} \)liegen dann auf verschiedenen Seiten von \( Z \). Fertige eine Skizze für \( m=-\frac{1}{2} \) an. Welcher Spezialfall ergibt sich für \( m=-1 ? \)
Problem/Ansatz:
a) Wie soll man den Streckungsfaktor ausdrücken außer, dass er angibt um welchen Faktor er das geometrische Objekt streckt?
b) Wird das Dreieck bei einer negativen zentrischen Streckung also verkleinert, aber was passiert bei m=-1?