Du kannst das mit starker Induktion machen.
Induktionsanfang. Der ist hier etwas gefährlich. Für n=2 ist die Aussage zunächst offensichtlich, für n=3 aber falsch, denn so ein Baum hat zwangsläufig einen Knoten mit Knotengrad 2. Nun hast du aber für n=2 einen Baum, der die Bedingung erfüllt. Setze deshalb an einen der Knoten zwei weitere Knoten wie im Bild an:
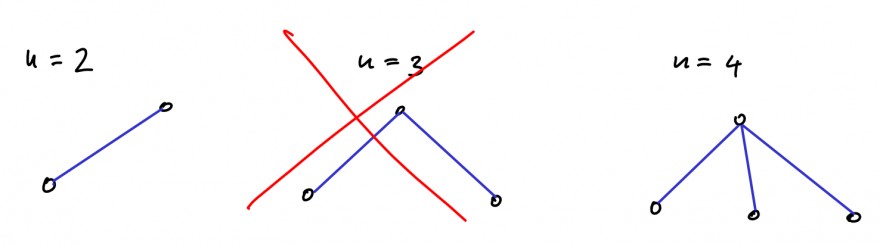
Induktionsvoraussetzung. Angenommen die Aussage gelte für alle \(k\leq n\in \mathbb{N}_{\geq 4}\cup \{2\} \). (IV)
Induktionsschritt. Also gilt diese Aussage auch für n+1 Knoten.
Jetzt hat man zwei Optionen:
1.) Du betrachtest im Baum aus der (IV) einen Knoten \(v\in V\) mit Knotengrad 1. Nach (IV) kannst du O.B.d.A annehmen, dass dieser Baum n-1 Knoten hat. Außerdem sei dieser Knoten \(v\) so gewählt, sodass dieser ein Kandidat für den (mindestens einen!) am längsten vorkommenden Pfad ist. Füge nun an diesen Knoten zwei neue Knoten \(v_1,v_2\) an, sodass diese nur über \(v\) miteinander in Verbindung stehen.
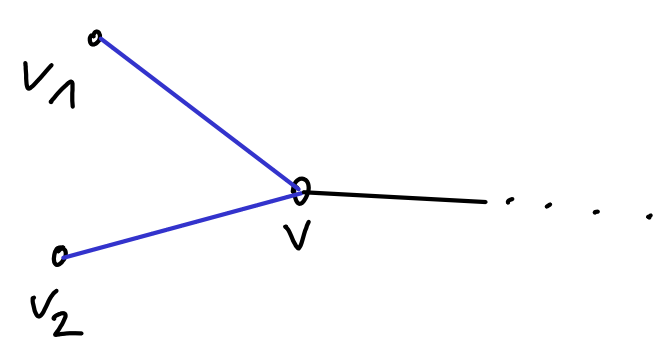
Dann gilt für diesen Knoten offenbar \(\deg(v)=3\neq 2\) und man hat einen Baum mit \(n+1\) Knoten. Nach (IV) hat dieser Baum einen längsten Pfad mit \(d\leq \frac{n-1}{2} \). Durch Anfügen von \(v_1,v_2\in V \cup \{v_1,v_2\}\) sind gerade diese beiden Konten um 1 von \(v\) entfernt und man erhält somit eine maximale Pfadlänge von \(d'\leq \frac{n-1}{2}+1=\frac{n+1}{2}\).
2.) Du betrachtest im Baum aus der (IV) einen Knoten\(v\in V\) mit \(\deg(v)>2 \). Den Rest kannst du dann analog wie in Fall 1.) konstruieren.