Hallo,
mache zunächst eine Zeichnung:
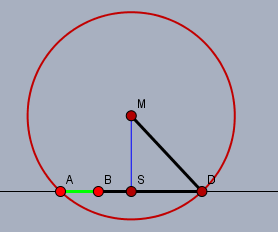
Die Sehne ist die Strecke \(AD\), der Radius \(r\) ist \(r=|MD| = |BD|\) und \(|MS|\) ist der Abstand der Sehne vom Mittelpunkt \(M\): \(|MS|=2\). Das Streckenstück \(|AB|\) hat die Länge \(1\). \(\triangle SDM\) ist ein rechtwinkliges Dreieck. Also gilt hier der Satz des Pythagoras, was dann auch zur Größe von \(r\) führt:$$\begin{aligned} \left(\frac{r+1}{2}\right)^2 + 2^2 &= r^2 \\ r^2 +2r +1 +16 &= 4r^2 \\ 3r^2 - 2r - 17 &= 0 \\ r_{1,2} &= \frac{2 \pm \sqrt{4 + 4 \cdot 3 \cdot 17}}{2 \cdot 3} \\ r_1 &= \frac 13(1 + 2\sqrt{13}) \approx 2,737 \end{aligned}$$Die geometrische Konstruktion geht wie folgt:
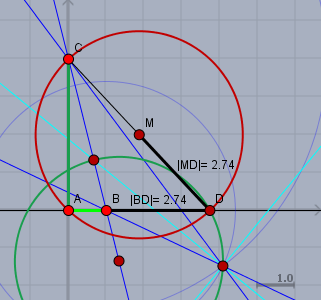
Zeichen das rechtwinklige Dreieck \(\triangle ABC\) mit den Katheten \(|AB|=1\text{cm}\) und \(|AC| = 2 \cdot 2\text{cm} = 4\text{cm}\). Konstruiere für die Strecke \(AB\) den Kreis des Appolloinos (grün) für das Verhältnis \(2 \div 1\). Bem.: \(|CD| = 2r = 2|BD|\). Dieser schneidet die Gerade durch \(AB\) über \(B\) hinaus in \(D\).
\(CD\) ist der Durchmesser des gesuchten Kreises. Die Strecken \(|MD|\) und \(|BD|\) sind so lang wie der gesuchte Radius \(r \approx 2,74 \text{cm}\).