Summe von Alpha-Fehler und Beta-Fehler minimieren

Question

 

wie kann man die Summe des Alpha- und Beta-Fehlers bei zwei Normalverteilungen welche sich schneiden (eine stellt die Nullhypothese die andere die Alternativhypothese dar) minimieren?

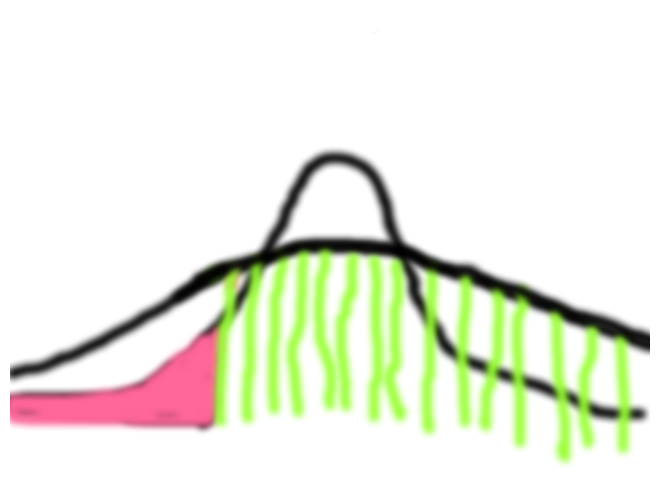
Ich habe versucht eine Skizze anzufertigen, ist mir leider nicht so gut gelungen. Jedenfalls soll der rote Bereich den Alpha-Fehler und der grün-schraffierte Bereich den Beta-Fehler darstellen.  Um jetzt die Summe der beiden Fehler zu minimieren fällt mir momentan die Möglichkeit ein, den kritischen Punkt nach rechts direkt zum linken Schnittpunkt der beiden Dichtefunktionen zu setzen.    Aber vielleicht gibt es doch noch ein andere Möglichkeit? z.B. über Ableitung?

 

Vielen Dank

Comments

Bei dir in der Skizze sieht es so aus als haben beide Hypothesen den gleichen Erwartungswert aber unterschiedliche Streuung. Das kann doch eigentlich nicht sein. Was hast du genau über die Normalverteilungen gegeben.

---

Ich gehe davon aus das beide Normalverteilungen verschiedene Erwartungswerte haben und sich ebenfalls in den Varianzen unterscheiden. Wobei die beiden Dichtefunktionen sich  in zwei Punkten schneiden. Die Skizze ist leider etwas undeutlich

Answer 1

Ich würde es in jedem Fall auch so sehen das der Schnittpunkt der Funktionen den Wert ergibt, wo die Summe der Fehler minimal wird.