Geschichte:
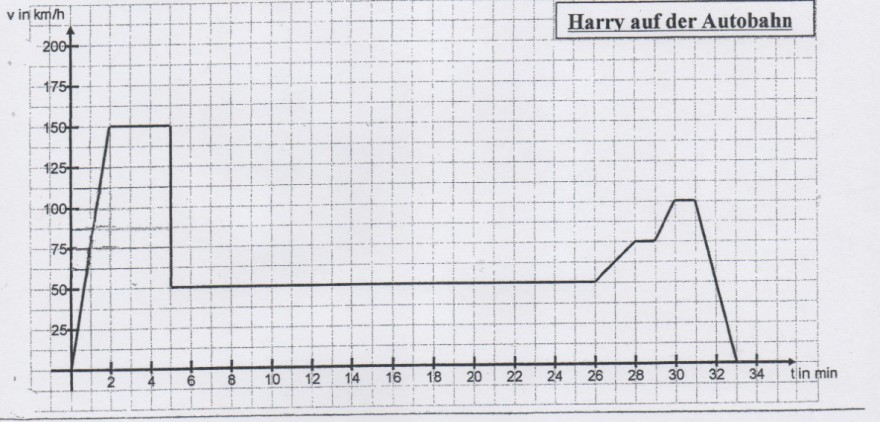
Harry ist immer noch dabei, Angelas Herz zu erobern. Er lädt sie daher in den größten Zoo (mit Streichelzoo) ein, der mit seinem neuen Auto und dem bentstandenen Führerschein nun gut erreichen ist. Der Taag verläuft allerdings nicht fanz wie erhofft... Als Angela ihm schließlich noch erzählt, dass sie sich gerade von ihrem Freund getrennt hat, sich dessen aber nun doch nicht so sicher ist, p0latzt Harry der Kragen. Er lässt Angela wutentbrannt stehen, verlässt den Zoo und schwingt sich in sein Auto. Die anderen Verkehrsteilnehmer sind ihm auf der Heimfahrt dann nur noch im Weg. (Harrys Fahrt ist etwas vereinfacht im Diagramm unten zu beobachten.)
Angela weiß dagegen gar nicht, wie ihr geschieht - mit Recht ist sie natürlich sauer. Ihr bleibt aber gar nichts anderes übrig als den 2 km entfernten Bahnhof zu Fuß mit 4 km/h anzusteuern. Dort muss sie dann glücklicherweise nur 10 Minuten auf den nächsten Zug warten - sie beabsichtigt Harry zur Rede zu stellen und fährt ihm daher nach. Ihr Zug legt nach 10 Minuten, 25 Minuten und 45 Minuten an Bahnhöfen jeweils eine zweiminütige Pause ein, die Fahrgeschwindigkeit beträgt 70 km/h. Nach weiteren 5 Minuten ist Angela schließlich am Ziehlbahnhof (Gesamte Fahrzeit im Zug: 52 Min)
Aufgaben:
1. Stelle Angelas Weg vom Zoo bis zum Zielbahnhof im t-v-Diagramm übersichtlich dar. Die Beschleunigungs- und Bremsphasen des Zuges sollen dabei unberücksichtigt bleiben bzw. als abrupt betrachtet werden.
2. Welchen Weg legt Angela vom Zoo bis zum Zielbahnhof zurück?
3. Beschreibe Harrys Fahrstil auf dem Heimweg in einem Text. Unterteile seine Fahrt dazu in sinnvole Abschnitte.
4. Welchen Weg legt Harry insgesamt zurück?
Problem/Ansatz:
1. Angelas Weg vom Zoo bis zum Zielbahnhof erfolgt durch zwei Schritte. Sie läuft erstens zum Bahnhof und dann fährt Sie mit dem Zug bis zum Zielbahnhof, demnach habe ich für ein besseres Zeichnen die Geschwindigkeiten, Strecken und ie Zeiten aufgestellt.
Lauf bis nach Bahnhof – s = 2 km; v = 4 km/h => t = s/v = 2 km / 4 km/h = ½ h
s = 2 km; v = 4 km/h; t = ½ h
Fahrt mit dem Zug bis zum Zielbahnhof – Beachtung, dass Angela zehn Minuten lang warten muss
Fahrtzeit t2 = 48 min; Geschwindigkeit v2 = 70 km/h => s2 = v2 * t2 = 70 km/h* 48 min ≈ 56 km, dabei Pausen nach 10 Minuten für 2 Minuten und weiterhin nach 25 und 45 Minuten
t2 = 0,87 h; s2 = 56 km; v2 = 70 km/h, dabei noch Pausen für zwei Minuten nach 10 (0,1 h), 25 (0,42 h) und 45 (0,75 h) Minuten
 Mein Graph zur Aufgabe
Mein Graph zur Aufgabe
 Aufgabe 2:
Aufgabe 2:
Die komplette Strecke von dem Zoo bis zum Zielbahnhof beträgt:
=> s1 = 2 km, s2 = 56 km
=> skomplett = s1 + s2 = 2 km + 56 km = 58 km
Antwort: 58 km beträgt ihr kompletter Weg von dem Zoo bis nach Zielbahnhof
Aufgabe 3: Ich denke, dass bis zum ersten Höhepunkt (2|150) Harry seinen Motor beschleunigt, deshalb sieht man in den ersten zwei Minuten eine lineare Steigung als Gerade bis zu dem Punkt. Dann fährt Harry weiter mit dieser Geschwindigkeit (150 km/h) für die weiteren drei Minuten, wahrscheinlich befindet er sich auf der Autobahn mit keinem Stau, denn in Deutschland fährt man nur mit dieser Geschwindigkeit häufig auf der Autobahn und das auch auf der linken Spur. Im weiteren Verlauf gelangt Harry wahrscheinlich im Stau für eine lange Zeit, man sieht dass sein Auto abrupt seine Geschwindigkeit ändert (auf 50 km/h) und dies konstant hält. Da er auf der Autobahn befindet, da seine Geschwindigkeit sich ändert und sie konstant beibehält, denke ich, dass er in einem geringem Stau sich befindet bzw. die Spuren wechselt. Ab dem Punkt (26|50) steigert seine Geschwindigkeit, ich denke, dass er auf der Autobahn eine andere Spur nimmt oder der Stau sich aufgelöst hat und zu seinem Ziel eilt. Ab dem Punkt Q (31|100) denke ich, dass er Richtung Autobahn-Ausgang fährt und wahrscheinlich zu seinem Haus eilt, da dieser Graph nur eine vereinfachte Version von seiner Fahrt ist.
Entschluss:
Beschleunigung des Motors (Fahrt Richtung Autobahn)
Auf Autobahn mit keinem Stau
Geringer Stau oder Spurwechsel
Ausgang Autobahn (Richtung Nähe des Zieles) und Ankunft
Aufgabe 4:
1. Abschnitt: s = v * t => s = 150 km/h * (2/60) h = 5 km
2. Abschnitt: s = v * t => s = 150 km/h * (3/60) h = 7,5 km
3. Abschnitt: s = v * t => s = 50 km/h * (21/60) h = 17,5 km
4. Abschnitt: s = v * t => s = 75 km/h * (2/60) h = 2,5 km
5. Abschnitt: s = v * t => s = 75 km/h * (1/60) h = 1,25 km
6. Abschnitt: s = v * t => s = 100 km/h * (1/60) h ≈ 1,67 km
Ich muss noch mit dieser Aufgabe fertig werden, aber stimmen die anderen Teilaufgaben?