Hallo wie löse ich diese Aufgabe?
Aufgabe:
Auch die Flugparabel bei einem schiefen Wurt kann man mit Hilfe des Unabhängigkeitsprinzips einfach konstruieren. Nehmen wir dazu an, dass jemand ein Ei mit \( 28,28 \mathrm{~m} / \mathrm{s} \) (knapp über \( 100 \mathrm{~km} / \mathrm{h} \) ) mit einem Winkel von \( 45^{\circ} \) abwirft und vemachlässigen wir wie immer den Luftwiderstand. Du wirst die schräge Zahl bei der Geschwindigkeit gleich verstehen. Fur die Vertikal- und Horizontalgeschwindigkeit bekommt man dann nämlich jeweils \( 20 \mathrm{~m} / \mathrm{s} \). Das lasst sich gut konstruieren!
Zuerst nehmen wir wieder an, dass keine Schwerkraft wirkt. Der Gegenstand würde dann geradlinig schräg nach oben fliegen (Abb. 6.12). Von diesen Positionen ziehen wir nun den freien Fall ab und schon ist die Wurfparabel fertig. Das Ei fliegt genau \( 80 \mathrm{~m} \) weit und steigt dabei \( 20 \mathrm{~m} \) hoch. Für einen Eierwurf auf fast \( 100 \mathrm{~m} \) ist daher eine größere Geschwindigkeit nötig.
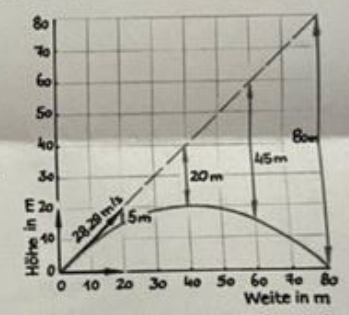
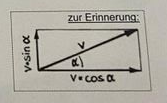
Abb. 6.12 schiefer Wurf mit einem Winkel von \( 45^{\circ} \). Die Teil-Komponenten kannst du mit dem Satz von Pythagoras ausrechnen oder mit Sinus und Cosinus.
Der günstigste Wurfwinket ist von der Weite unabhängig und liegt bei \( 45^{\circ} \). Bei Winkeln, die einander auf \( 90^{\circ} \) ergänzen ist die Wurfweite gleich groß. Mit \( 50^{\circ} \) wirfst du also gleich weit wie mit \( 40^{\circ} \) und mit \( 60^{\circ} \) so weit wie mit \( 30^{\circ} \)
Der Weltrekord im Eierwurf liegt laut Guinness Buch bei \( x=98,5 \mathrm{~m} \) (das Ei wurde angeblich sogar gefangen ohne, dass es zerbricht). Bestimme die Abwurfgeschwindigkeit \( v_{0} \). die dafür notwendig ist.