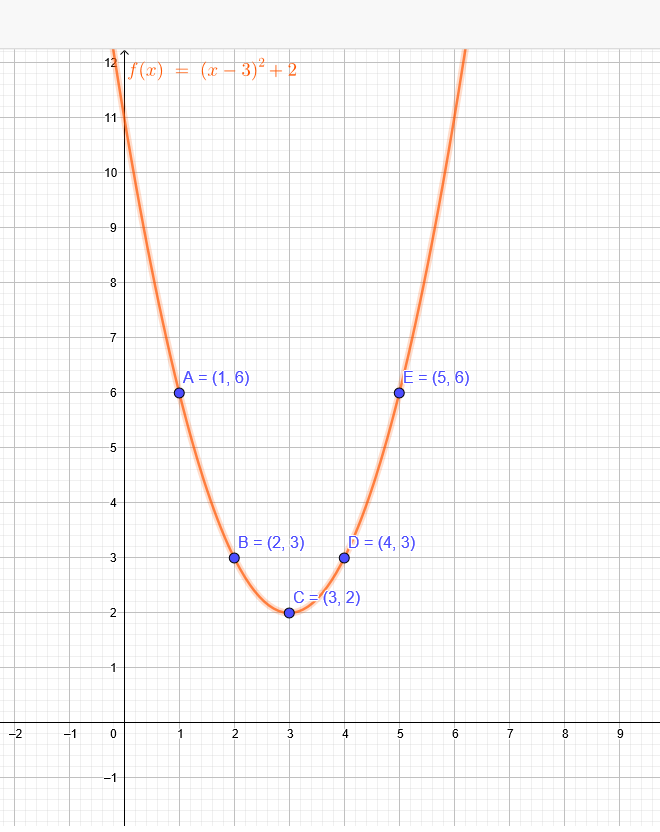
Finden Sie das Polynom mit Grad 2 so dass sein Graph die Punkte (1,6), (2,3), (3,2) beinhaltet.

Question

Aufgabe:

Finden Sie das Polynom mit Grad 2 so dass sein Graph die Punkte (1,6), (2,3), (3,2) beinhaltet.

Problem/Ansatz:

Graphen

Answer 1

f(x)=ax^2 + bx + c

mit f(1)=6 ==>   a + b + c = 6

   f(2)=3  ==>  4a + 2b + c = 3

      etc. gibt 3 Gleichungen für a,b und c.

Comments

Prima,

Answer 2

Finden Sie das Polynom mit Grad 2 so dass sein Graph die Punkte A(1|6), B(2|3), C(3|2) beinhaltet.

Ich verschiebe die Punkte um 2 Einheiten nach unten:  A´(1|4), B´(2|1), C´(3|0)

In C´(3|0) liegt das Minimum: doppelte Nullstelle

y =  a * ( x - 3 ) ^ 2

A´(1|4)

y(1) =  a * (1 - 3 ) ^ 2

a * (1 - 3 ) ^ 2 = 4

a = 1

y = ( x - 3 ) ^ 2  Nun wieder 2 Einheiten nach oben

p(x)=( x - 3 ) ^ 2+2

mfG Moliets

Comments

Hochelegant!

---

Das hat bei deiner Aufgabe geklappt, aber in folgendem Falle ergibt es eine Hyperbel.

Meines Wissens ist das aber kein Polynom2. Grades.

mfG

Moliets

---

Ja, klar!

Es war interessant!