Quadratische Gleichungen: ist das so richtig oder ist da ein Denkfehler? (komische Lösungszahlen)

Question

(7+s)² =24+s

s²+14s+49=24+s |-24-s

s²+13s+25=0 |P.q.

s1,s2=-7,5+,-\( \sqrt{x} \)56,25-25

s1= 1,90983    s2= -13,0902

Wir haben einen Mathezettel mit 45  Quadratischen Gleichungen bekommen, die wir lösen sollen. Da haben einige so komische Zahlen als Lösung wie diese hier. Deswegen wollte ich mal als Beispiel dieser fragen, ist das so richtig oder ist da ein Denkfehler? Das s auf der rechten Seite versaut halt ein schönes Ergebnis :/

Answer 1

Die vierte Zeile ist unverständlich, die fünfte Zeile ist falsch.

Answer 2

(7+s)² =24+s

49+14s+s^2=24+s

s^2+13s =  -  25 

(s+6,5)^2=  - 25+6,5^2=17,25

s_1=-6,5+4,15=-2,35

s_2=-6,5-4,15=-10,65

mfG

Moliets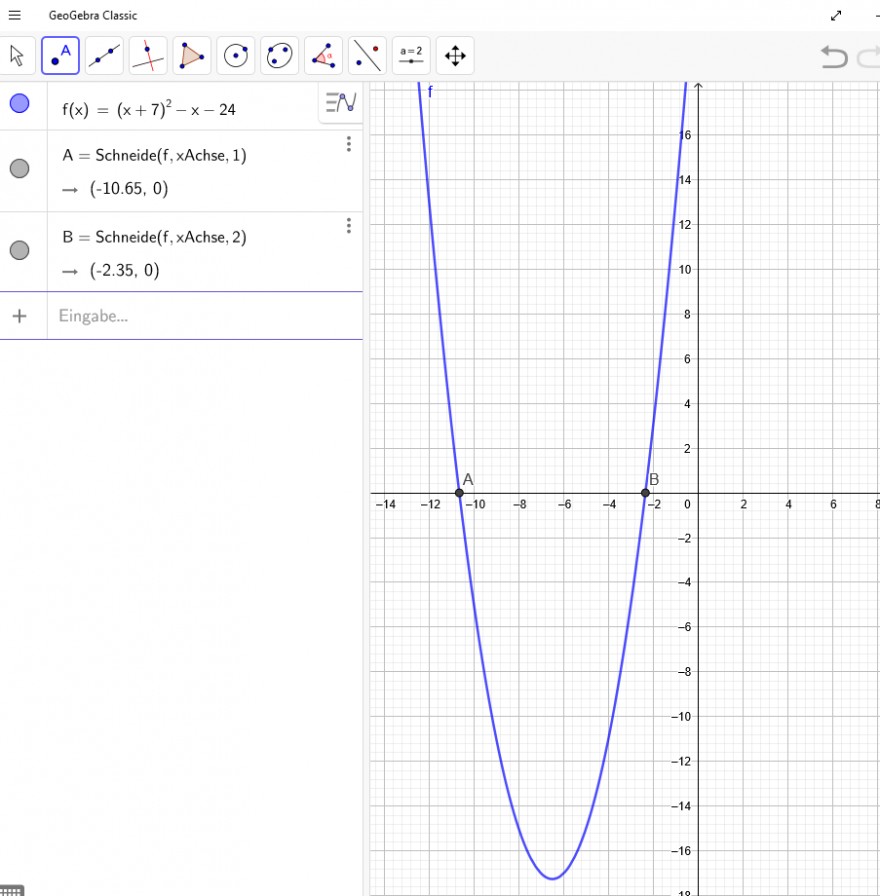

Text erkannt:

\( \equiv \) GeoGebra Classic
\( f(x)=(x+7)^{2}-x-24 \)
\( =N \)
\( \mathrm{A}=\mathrm{Schneide}(\mathrm{f}, \times \mathrm{Achse}, 1) \)
\( \vdots \)
\( \rightarrow(-10.65,0) \)
\( \mathrm{B}= \) Schneide \( (\mathrm{f}, \times \) Achse \( , 2) \) :
\( \rightarrow(-2.35,0) \)
ingabe.

Answer 3

s²+13s+25=0

$$s_{12}=-6,5\pm\sqrt{42,25-25}$$

Answer 4

Hallo,

bis zur dritten Zeile ist ja soweit alles in Ordnung,

nur 13 : 2 = 6,5   und nicht wie hier 7,5

damit ist s _1,2 =  -6,5 ±\( \sqrt{6,5²-25} \)

und da kommt wirklich nichts glattes raus

   s_1,2=  -6,5 ± 4,1533