Radius und Höhe beim Kegel berechnen

Question

Aufgabe: Ein Designer soll ein Sektglas mit kegelförmigem Füllbereich entwerfen. Die Seitenlinie des Füllbereiches ist mit einer Länge von 12 cm vorgegeben.

Berechnen Sie die übrigen Maße Radius und Höhe, so dass das Volumen des
Füllbereiches maximal wird.

Problem/Ansatz:

Wie berechnet man aus der Seitenlänge den Radius und die Höhe?

Answer 1

Hallo,

die Mantellinie kann mit der Höhe und dem Radius des Kegels über den Satz von Pythagoras in Zusammenhang gesetzt werden. Es gilt \(12^2=h^2+r^2\).

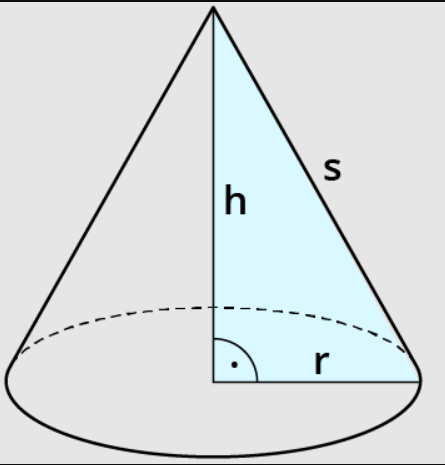
Die Volumenfunktion ist \(V(r,h)=\frac{1}{3}\pi\cdot r^2\cdot h\). Setzt du die Nebenbedingung, die ich eben mit dem Satz von Pythagoras begründet habe, in diese Funktion ein, so hast du: $$V(h)=\frac{1}{3}\pi (12^2-h^2)\cdot h$$

Comments

[spoiler]

\( \max \left\{\frac{1}{3} \pi\left(\left(12^{2}-h^{2}\right) h\right)\right\} \approx 696.50 \) at \( h \approx 6.9282 \)

[/spoiler]

Answer 2

(1) V=1/3·π·r²·h

r²+h²=144 oder (2) r²=144-h²

(2) in (1) einsetzen, ergibt

V(h)=π·(48h-h³/3)

Die positive Nullstelle der ersten Ableitung ist die gesuchte Höhe h des Glases. h in (2) eingesetzt ergibt den Radius r des Glases.