Berechnen sie den Abschusswinkel.

Question

Aufgabe:

Beim Tontaubenschießen auf ebenem Gelände wird die Flugbahn durch eine Parabel angenähert. Ein Abschussgerät erreicht eine Weite von 100m und 40m maximale Höhe.

a) Berechnen sie den Abschusswinkel.

b) Ein Zuschauer steht direkt unter dem Gipfelpunkt der Bahn auf einem 2m hohen Podest. In welchem Punkt ihrer Flugbahn ist ihm die Tontaube am nächsten?

Problem/Ansatz:

Hallo, mein Ansatz wäre die Funktionsgleichung. Ich bin mir nicht ganz sicher, ob sie richtig ist und wie ich damit weiter arbeiten kann.

f(x)= -0,016x²+1,6x

Answer 1

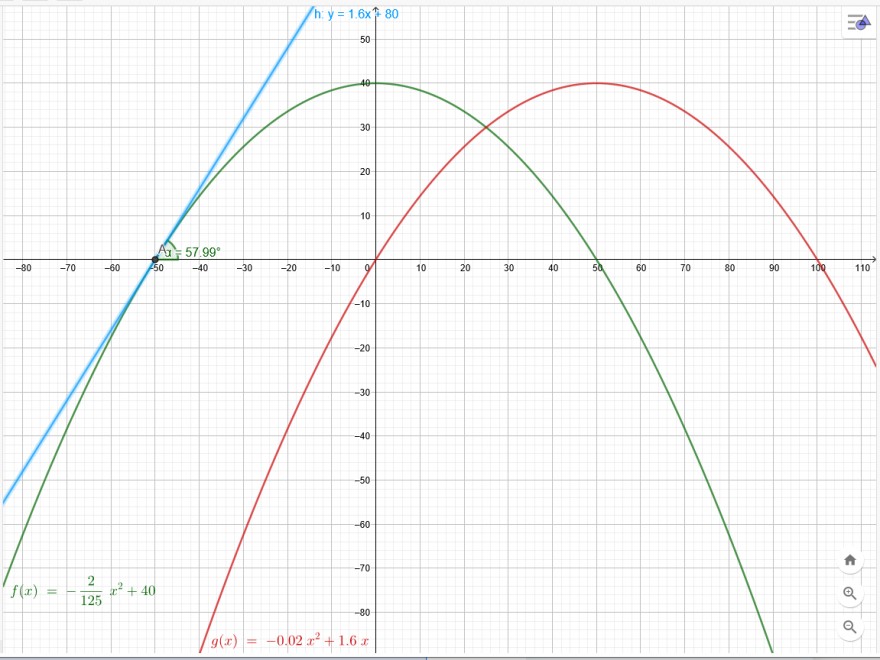
Scheitelform der Parabel

f(x)=a*x^2+40

f(50)=a*2500+40

a*2500+40=0

a=-\( \frac{2}{125} \)

f(x)=-\( \frac{2}{125} \)*x^2+40

f´(x)=-2*\( \frac{2}{125} \)*x

f´(-50)=-2*\( \frac{2}{125} \)*(-50)=\( \frac{200}{125} \)=\( \frac{8}{5} \)=1,6

Winkel :    tan^-1(1,6)=57,99°

Deine Parabelgleichung stimmt auch. (Ich habe beide Parabeln aufgezeichnet.)

Comments

Ist sehr gut nachzuvollziehen. Wie kann ich damit in Aufgabe b) weitermachen?

---

Text erkannt:

\( f(x)=-\frac{2}{125} x^{2}+40 \)
\( f^{-}(x)=-\frac{4 x}{125} \)
\( \frac{y-2}{x-0}=\frac{125}{4 x} \)
\( 4 y-8=125 \)
\( y=\frac{133}{4} \)
\( -\frac{2}{125} x^{2}+40=\frac{133}{4} \)
\( x_{1}=\ldots \)
\( x_{2}=\ldots \)
\( B \) und \( C \) sind die nächsten Punkte. (Zeichnung)