Question

Berechne den Flacheninhalt des dargestellten Trapezes.

Können Sie bitte mir helfen ich habe morgen test ind ich verstehe diese aufgabe nicht

Text erkannt:

6. Berechne den Flacheninhalt des dargestellten Trapezes.

Answer 1

cos(100°-90°)=cos(10°)=\( \frac{h}{d} \)      h=cos(10°)•20

Strecke A E:  sin10°= \( \frac{Strecke A E}{20} \)       A E =20•sin(10°)

Strecke F B: ....

u.s.w.

Comments

Ich habe das nicht gut verstanden

---

Ich habe das nicht gut verstanden

möchtest Du selber knobeln oder eine vollständige Lösung?

---

Komplett weil wenn ich so mache ich weiß nicht ab meine ergibniss falsch oder nicht

---

So Strecke F B: ist 8m ja?

Weil 20-12=8m

---

Weil 20-12=8m

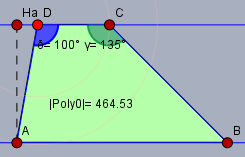
Nein - betrachte das Dreicke \(\triangle FBC\). Dort gilt$$\tan 45° = \frac{|FB|}{|FC|} \\\implies |FB| = |FC| \cdot \tan 45° = |FC|$$und die Strecke \(|FC|\) ist die Höhe \(h\) des Trapez'. Mit \(h = 20 \cos(10°)\) ist auch $$|FB| = 20 \cdot \cos(10°) \approx 19,70$$Die Strecke \(|AE|\) bekommt man im dreieck \(\triangle AED\) über $$|AE| = 20 \cdot \sin(10°) \approx 3,47$$und \(|AB|\) ist die Summe von $$|AB| = |AE| + |EF| + |FB| = 3,47 + 12 + 19,7 = 35,17$$Damit hast Du die beiden parallelen Seiten und die Höhe des Trapez und kannst die Fläche berechnen$$F = \frac 12(|AB| + |DC|) h \approx 464,5$$Mache Dir auch immer eine Zeichnung