Vollständige Induktion benötige Lsg

Question

Aufgabe

Vollständige Induktion

Problem/Ansatz:

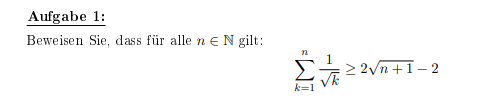
Text erkannt:

\( \frac{\text { Aufgabe 1: }}{\text { Beweisen Sie, dass für alle } n \in \mathbb{N} \text { gilt: }} \)
$$ \sum \limits_{k=1}^{n} \frac{1}{\sqrt{k}} \geq 2 \sqrt{n+1}-2 $$

Benötige die Lösung bzw. den Lösungsweg zu dieser Aufgabe versuche eine Formelsammlung zu erstellen und würde gerne einige Aufgabentypen einer Induktion vollständig sehen. Vielen dank im Voraus!

Answer 1

Hallo,

zu zeigen ist:$$\sum \limits_{k=1}^{n} \frac{1}{\sqrt{k}} \geq 2 \sqrt{n+1}-2 $$Induktionsanfang ist klar. Für \(n=1\) ist $$\begin{aligned}\sum \limits_{k=1}^{1} \frac{1}{\sqrt{k}} &\geq 2 \sqrt{1+1}-2 \\ 1 &\geq 2\sqrt 2 - 2 \lt 0,8 \space \checkmark\end{aligned}$$Der Induktionschritt ist ein wenig tricky. Man muss wissen wo man hin will:$$\begin{aligned} \sum_{k=1}^{n+1} \frac{1}{\sqrt{k}} &= \sum_{k=1}^{n} \frac{1}{\sqrt{k}} \space + \frac{1}{\sqrt{n+1}} \\  &\geq 2 \sqrt{n+1}-2 + \frac{1}{\sqrt{n+1}} &&|\, \text{lt. Voraussetzung} \\ &= \frac{2(n+1) + 1}{\sqrt{n+1}} - 2 \\ &= \frac{2n+3}{\sqrt{n+1}} - 2 \\ &= 2\frac{n+\frac 32}{\sqrt{n+1}} - 2 \\ &= 2\frac{\sqrt{\left(n+\frac 32\right)^2}}{\sqrt{n+1}} - 2 \\ &= 2\frac{\sqrt{n^2 + 3n + \frac 94}}{\sqrt{n+1}} - 2 &&|\, \frac 94 \gt 2\\ &\gt 2\frac{\sqrt{n^2 + 3n + 2}}{\sqrt{n+1}} - 2 \\ &= 2\frac{\sqrt{(n+1)(n+2)}}{\sqrt{n+1}} - 2 \\ &= 2\sqrt{n+2} - 2 \\ &\text{q.e.d.} \end{aligned}$$