Hallo:-)
Leider ist diese Aussage zu schwach formuliert, sodass sie allgemein nicht richtig ist. Ich habe mal ein paar zusammenhängende Graphen dazu aufgemalt:
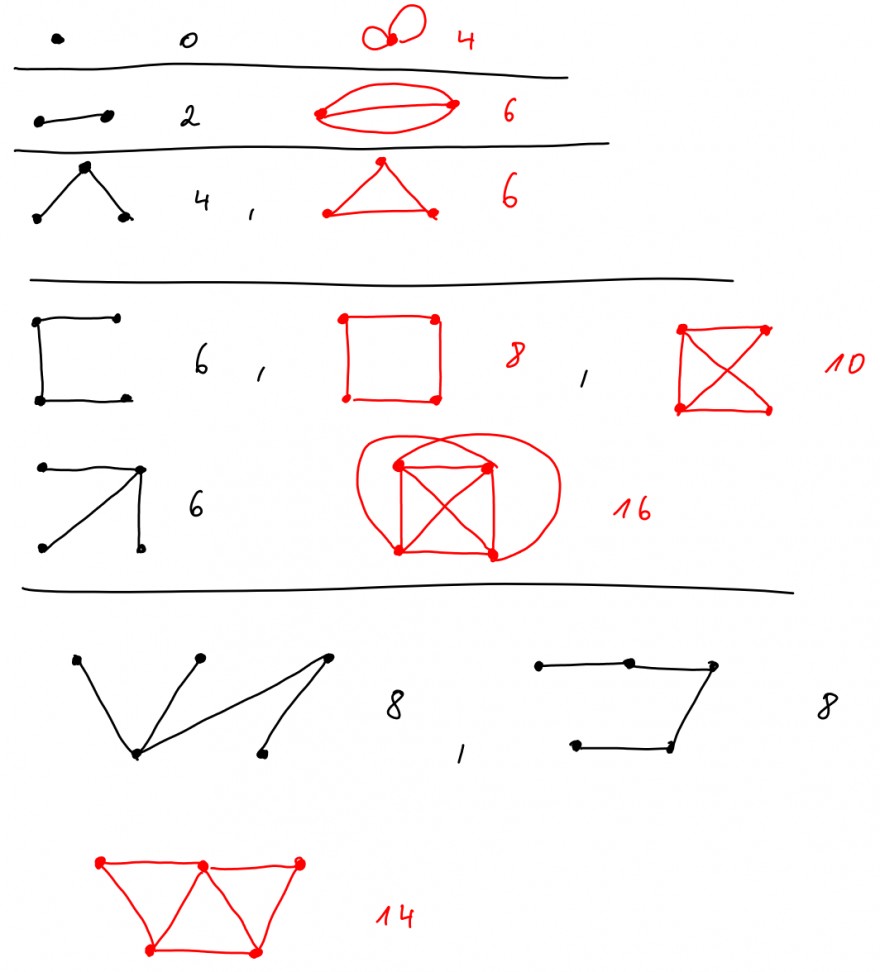
Neben jedem Graphen steht die Summe aller Knotengrade. Die schwarzen Graphen sind die Graphen, die die Aussage erfüllen, die roten sind zwar auch zusammenhängend, erfüllen die Aussage jedoch nicht.
Was aber an allen schwarzen Graphen auffallend ist, dass diese minimal zusammenhängend sind. Das bedeutet: Entfernt man eine Kante, so zerfällt der Graph in zwei disjunkte Teilgraphen. Außerdem sind diese einfach (höchstens eine Kante zwischen je zwei Knoten). Das ist äquivalent dazu, dass alle schwarzen Graphen hier Bäume sind.
Also muss deine Aussage stärker formuliert werden:
Für jeden Graphen \(G\) mit Knotenmenge \(V(G)\), der Baum ist, gilt
\(\sum\limits_{v\in V(G)}\deg(v)=2(|V|-1)\).