Höhe, Flächeninhalt und Volumen berechnen

Question

                                                                                    

Vom Querschnitt eines Deiches sind die folgenden Maße bekannt:

k = 2,80m, u = 20m, α = 15°, β = 35°,

Berechne

a) die Höhe h des Deiches und die Breite a der Deichsohle

b) den Flächeninhalt des Deichquerschnitts und das Volumen an Material  für einen  250m langen Deich.

 

Zu dieser Aufgabe finde ich momentan leider keinen Ansatz. 

Hilfe wäre ganz klasse!

Danke und Gruß,

Sophie

Answer 1

Zunächst eine etwas ergänzte Skizze:

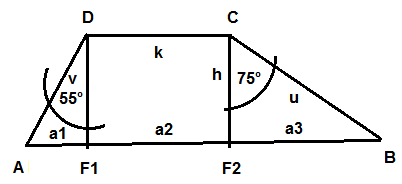
a) Der Winkel bei C muss 75 ° betragen (warum?).

Damit erhält man:

h / u = cos ( 75 ° )

<=> h = u * cos ( 75 ° ) = 20 * cos (  75 ° ) = 5,18 m

und

a3 / u = sin ( 75 ° )

<=> a3 = u * sin ( 75 ° ) = 20 * sin ( 75 ° ) = 19,32

 

Der Winkel bei D muss 55 ° betragen (warum?).

Damit erhält man

h / v = cos ( 55 ° )

<=> v = h / cos ( 55 ° ) = 8,72 m

und damit auch :

a1 / v = sin ( 55 ° )

<=> a1 = v * sin ( 55 ° ) = 8,72 * sin ( 55 ° )  = 7,14 m

 

Außerdem gilt:

a2 = k = 2,8 m

sodass für die Gesamtlänge a der Deichsohle gilt:

a = a1 + a2 + a3 = 7,14 + 2,8 + 19,32 = 29,26 m

 

b) Der Flächeninhalt A eines Trapezes ergibt sich aus der Formel

A = ( a + c ) * h / 2

wobei a und c die Längen der parallelen Seiten des Trapezes bezeichnen, hier also:

a = 29,26 und c = k = 2,8 , also:

A = ( 29,26 + 2,8 ) * 5,18 / 2 =  83,04 m ²

Für einen Deich mit der Länge L = 250 m wird

V = A * L = 83,04 * 250 = 20760 m ³

Material benötigt.