Hallo Julian,
die häufigsten Formen für Beweise sind der direkte Beweis, der indirekte Beweis (auch Beweis durch Widerspruch) und vielleicht noch der Beweis über Induktion. Letzteres ist auch ein direkter Beweis.
Bei jedem Beweis geht es um eine Aussage, wie "die Summe der Quadrate der Katheten in einem rechtwinkligen Dreieck ist genauso groß wie das Qudrat der Hypotenuse". Diese Aussage kann man nur beweisen, wenn man sich auf bestimmten Voraussetzungen abstützt. Z.B. an Hand dieser geometrischen Figur:
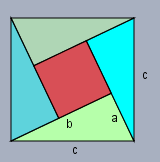
Die Voraussetzung ist hier, dass die vier rechtwinkligen Dreiecke gleich groß sind und dass die Summe der Flächen der vier Dreiecke plus der Fläche des roten Quadrat die Fläche des umhüllenden Quadrats \(c^2\) ergibt. Das geschieht über eine Folge von logischen Schlüssen, die am Ende zu der Aussage oben führen.
Kann mir jemand ein Beispiel machen für Beweise,also wie man etwas beweist.
Die Fläche eines Dreiecks ist \(F_{\triangle}=a\cdot b\). Die Fläche des roten Quadrats ist \(F_q=(b-a)^2\) Und die Fläche des großen umhüllenden Quadrats ist \(F_Q=c^2\). Mit obiger Voraussetzung, dass sich die Flächen passgenau zusammen legen lassen, gilt$$\begin{aligned}4F_{\triangle} + F_q &= F_Q\\ 4\cdot \frac 12 a\cdot b + (b-a)^2 &= c^2\\ 2ab + b^2 - 2ab + a^2 &=c^2\\ a^2+b^2 &= c^2\end{aligned}$$und da steht formal das, was oben behauptet wurde. Damit ist der Satz des Pythagoras bewiesen!
Beim Beweis mit Widerspruch nimmt man das Gegenteil dessen an, was man Beweisen möchte und zeigt, dass das nicht möglich ist. Ein berühmtes Beispiel ist der Beweis, dass es unendlich viele Primzahlen gibt. Hier nimmt man an, dass dem nicht so ist. Daraus folgt, dass es ein größte Primzahl geben muss. Und anschließend zeigt man, dass das nicht wahr ist, weil sich zu jeder beliebig großen Primzahl noch eine größere finden lässt.
Mit dem Beweis per Induktion beweist man Aussagen, die i.A. eine Zahl \(n\) enthalten. Man zeigt, dass die Aussage für eine kleine Zahl - z.B. \(n=1\) - korrekt ist. Anschließend zeigt man dann - wieder durch logische Folgerungen - dass die Aussage auch für \(n+1\) gilt, wenn sie für \(n\) gilt.
Zum Beispiel gilt: die Summe aller (natürlichen) Zahlen von \(1\) bis \(n\) ist$$\sum\limits_{k=1}^n k = 1+2+ \dots + (n-1) + n = \frac 12 n(n+1)$$Das zeigt man zunächst für \(n=1\). Die Summe der einen Zahl von \(1\) bis \(1\) ist natürlich \(1\). Und die Formel stimmt auch:$$1 = \frac 12 \cdot 1 \cdot (1+1) = 1 \space \checkmark$$Also nehmen wir an, dass es für \(n\) stimmt. Dann betrachtet man das für \(n+1\)$$\begin{aligned}\sum\limits_{k=1}^{n+1} k &= \underbrace{1 + 2 + \dots + (n-1) + n}_{\sum_{k=1}^n k} + (n+1) \\ &= \sum\limits_{k=1}^n k \quad + (n+1) \\&= \frac 12n(n+1) + (n+1) \\&= \left( \frac 12 n + 1 \right) (n+1) \\&= \frac 12(n+2)(n+1) \\&= \frac 12(n+1)((n+1) + 1)\end{aligned}$$wie man sieht, stimmt die Formel auf für \(n+1\) wenn sie für \(n\) stimmt. D.h. da sie für \(n=1\) richtig ist, muss es auch für \(n=2\) gelten. Und da es für \(n=2\) ok ist, ist es auch für \(n=3\) richtig usw.
Falls Du dazu noch Fragen hast, so melde Dich bitte.
Gruß Werner