Aufgabe:

Text erkannt:
14 Ein Ballon startet im Punkt A(21510). Er bewegt sich geradlinig mit konstanter Geschwindig. keit und ist nach einer Stunde im Punkt B (4|8|1). Beim Start des Ballons befindet sich ein Kleinflugzeug im Punkt \( C(10|15| 1) . \) Der Vektor \( \vec{u}=\left(\begin{array}{r}-30 \\ -60 \\ 60\end{array}\right) \) gibt die Veränderung seiner Position in einer Stunde an. Die Koordinaten sind in Kilometern angegeben.
a) Wie weit ist der Punkt \( C \) vom Startplatz A des Ballons entfernt?
b) Überprüfen Sie rechnerisch, ob sich die Flugbahnen von Ballon und Flugzeug kreuzen und ob sie kollidieren können.
c) Mit welcher Geschwindigkeit fliegen der Ballon bzw. das Flugzeug?
d) Welche Annahmen werden für die hier beschriebene Situation gemacht? Halten Sie diese für realistisch? Begründen Sie Ihre Antwort.
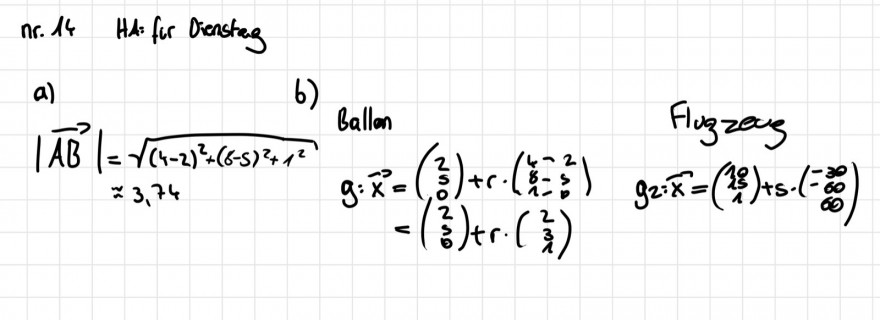
Text erkannt:
nr. \( 14 \quad H A \) fur Oenstrag

Text erkannt:
\( \left(\begin{array}{l}2 \\ 5 \\ 0\end{array}\right)+r \cdot\left(\begin{array}{l}2 \\ 3 \\ 1\end{array}\right)=\left(\begin{array}{c}18 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{c}-\frac{30}{-\infty} \\ -\infty\end{array}\right) \)
\( \left.\begin{array}{l}2+2 r=10-30 s 1 \cdot 2 \\ s+3 r=15-60 s \\ r=1+60= \\ 4+4 r_{0} 20-60 s\end{array}\right] \)
\( \begin{aligned} 1-r &=-s \quad 1-1 \\-r &=-6 \quad \mid:(-1) \\ r &=6 \end{aligned} \)
\( \begin{aligned} 2+2.6 &=10-30 s \\ 14=10-30,1-10 \\ 4 &=-30 \mathrm{~s} \quad \mid:(-30) \\-\frac{2}{15} &=s \end{aligned} \)
C) \( \begin{aligned}|\tilde{v}| &=\sqrt{30^{2}+60^{2}+60^{2}} \\ & \approx 90 \end{aligned} \)
=o oie Geschuindigkeit
betrigh \( 90 \mathrm{kmlR} \).
d) ?
Problem/Ansatz:
… Ich wollte fragen, ob ich die Aufgabe richtig habe. Ich wollte auch fragen, wie d) geht