Vom Duplikat:
Titel: Rechteck konstruieren mit längen
Stichworte: geometrie,konstruieren,rechteck
Upload failed: [object Object]
Aufgabe:
Problem/Ansatz:
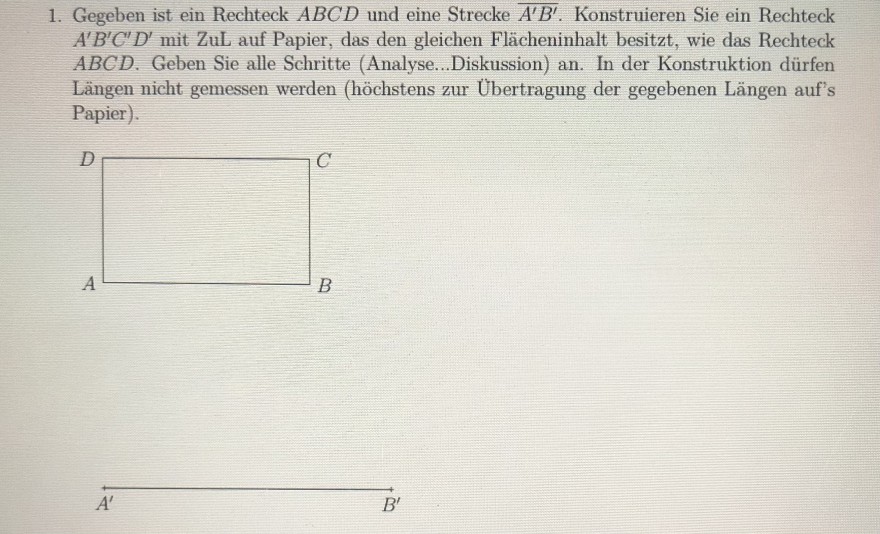
Text erkannt:
1. Gegeben ist ein Rechteck \( A B C D \) und eine Strecke \( \overline{A^{\prime} B^{\prime}} \). Konstruieren Sie ein Rechteck \( A^{\prime} B^{\prime} C^{\prime} D^{\prime} \) mit \( Z u L \) auf Papier, das den gleichen Flächeninhalt besitzt, wie das Rechteck \( A B C D \). Geben Sie alle Schritte (Analyse...Diskussion) an. In der Konstruktion dürfen Längen nicht gemessen werden (höchstens zur Übertragung der gegebenen Längen auf's Papier).