a) Erste Ableitung gleich Null setzen.
b) Zweite Ableitung gleich Null setzen.
--> xW
--> f'(xW) liefert die Steigung mT der Wendetangente.
→ mW=-1/mT ist die Steigung des Wanderwegs.
--> g(x)=mW*(x-xW)+yW
Erst einmal ein Bild.
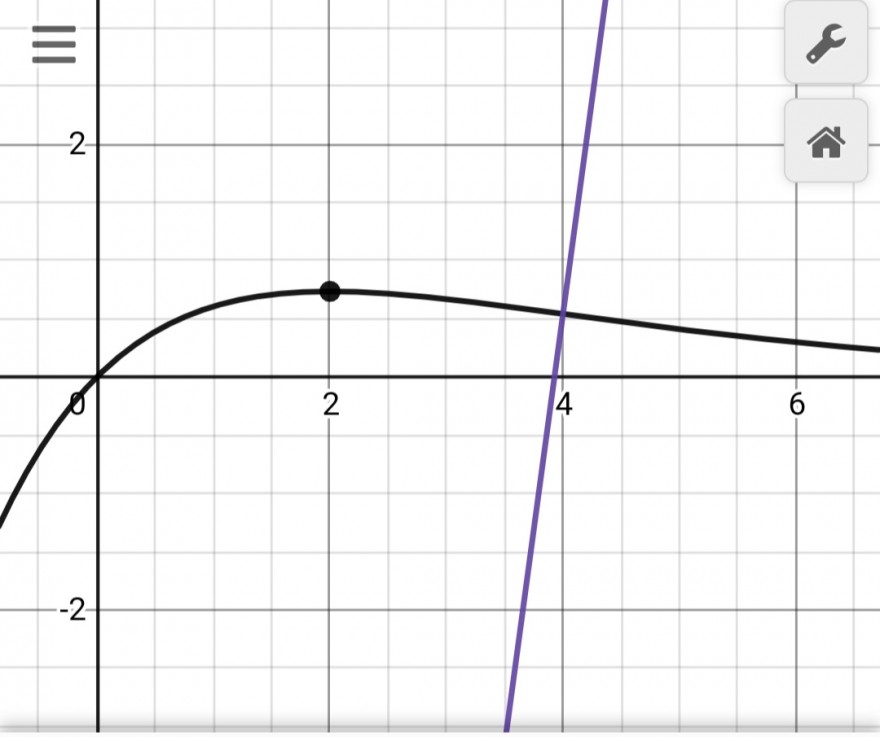
Du brauchst die Ableitungen.
f(x) = x*e^{-0,5x}
f'(x) = 1*e^{-0,5x}+x*(-0,5*e^{-0,5x})
f'(x)=(1-0,5x)*e^{-0,5x}
f''(x)= -0,5*e^{-0,5x}+(1-0,5x)*(-0,5)*e^{-0,5x}
f''(x)=(-1+0,25x)*e^{-0,5x}
Nun zu a)
f'(x)=0 → 1-0,5x=0 → x=2
y=f(2)=2/e≈0.736 kannst du mit dem Taschenrechner bestimmen.
P(2|0,736)
Zu b)
f''(xW)=0 → -1+0,25xW=0 → xW=4
yW=f(4)=4/e^2≈0,541 mit Taschenrechner.
mW=-1/f'(4)≈7,389 ebenfalls.
Die Gleichung des Wanderwegs:
g(x)=mW*(x-xW)+yW
Nun noch die Zahlen einsetzen.
g(x)=7.389*(x-4)+0.541
\( g(x)=7.389 x-29.015 \)
Fertig.
:-)