Ich möchte zuerst etwas zeigen:
Hier sagt das Buch wann man diese Diagramme benutzen:
NUR ZUM SEHEN
1)

Text erkannt:
Vetpa In einem Kreisdiagramm entsprechen die Winkelgrößen der Kreisausschnitte den dargestellten Zahlen. Kreisdiagramme eignen sich nur, wenn die Aufteilung eines Ganzen in bestimmte Anteile darzustellen ist. \( \quad \) \& Lop
(1) Beschreibung Das abgebildete Kreisdiagramm gibt den prozentualen Anteil an Wohnungen mit \( 1,2, \ldots, 7 \) und mehr Wohnrăumen in Sachsen am 31. 12. 2002 wieder. Die absolute Anzahl an Wohnungen, auf die die Prozentangaben Bezug nehmen, ist nicht genannt.
(2) Auswertung hecteht aus vier. knapp unter einem Drittel aus drei Wohn-
2)

Text erkannt:
6.2 Säulendiagramme
In einem Säulendiagramm entsprechen die Längen der Säulen den dargestellten Zahlen oder Gröben. Die Säulen müssen dabei gleich breit sein, damit die Darstellung beim Betrachter keinen falschen Eindruck erzeugt. Saulendiagramme eignen sich besonders gut, um verschiedene Größen und Anzahlen anschaulich vergleichen zu können - z. B. in ihrer zeitlichen Entwicklung. Werden die Säulen nicht senkrecht, sondern waagerecht gezeichnet, spricht man auch vom Balkendiagramm.
(1) Beschreibung Das abgebildete Săulendiagramm gibt die Anzahl der Studierenden in Sachsen in den Jahren von 1993 bis 2002 wieder. Dabei werden die absoluten Zahlen in Tausende zusammengefasst und dargestellt. Das Diagramm muss aus dem Jahr 2003 oder später stammen, da es sich bei den Werten nicht um Prognosen handelt.
3)
Text erkannt:
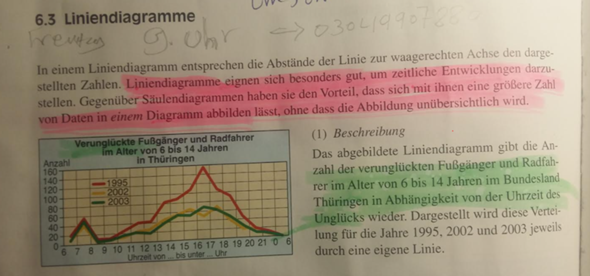
6.3 Liniendiagramme
In einem Liniendiagramm entsprechen die Abstände der Linie zur waagerechten Achse den dargestellten Zahlen. Liniendiagramme eignen sich besonders gut, um zeitliche Entwicklungen darzustellen. Gegenüber Săulendiagrammen haben sie den Vorteil, dass sich mit ihnen eine gröBere Zahl von Daten in einem Diagramm abbilden lässt, ohne dass die Abbildung unübersichtlich wird.
(1) Beschreibung Das abgebildete Liniendiagramm gibt die Anrer im Alter von 6 bis 14 Jahren im Bundesland Thüringen in Abhăngigkeit von der Uhrzeit des Unglücks wieder. Dargestellt wird diese Verteilung für die Jahre 1995,2002 und 2003 jeweils durch eine eigene Linie.
HIer fängt die Aufgabe an.
1) meine Begründung für das linke Diagramm stimmt? ok
2) für das rechte Diagramm:
Hier bezüglich das Kreisdiagramm auch ok, aber für
das Liniendiagramm , Dein Zitat "" Mir ist klar, dass du die Begründung einfach vom ersten Diagramm kopiert hast, was auch kein Problem wäre, wenn es einen Vergleich gäbe.""
HIer habe ich eine Frage. Also meinst du Beispiel beim linken Diagramm, ja gibt es Vergleiche , weil dort geht es um die Anzahl der Verunglückten im Laufe des Jahres ( pro Monat) also wie entwickelt sich diese Größe oder Zahl (Anzahl der Verunglückten) vo Monat zu Monat. Deshalb ( Es gibt ein Verglich)
ABER beim rechten Diagramm , gent es NICHT um eine Größe oder Zahl , wo man die pro Monat oder so vergleichen kann, sonder geht es um MEHRERE oder Zahlen, nämlich
(Kopflausfall; Plitzfektion; Kurz nd Weitsichtigkeit uw.......) Deswegen kann ich hier NICHT sagen. " es geht um Größen oder Zahlen zu verglichen, also es gibt keinen Vergleich" Daher passt NICHT Liniendiagramm nicht für das rechte Diagramm? Stimmt.
Natürlich passt hier Liniendiagramm ,weil hier keine zwichenwertde gibt, das ist klar
Bezüglich des Kreisdiagramms ist klar.
