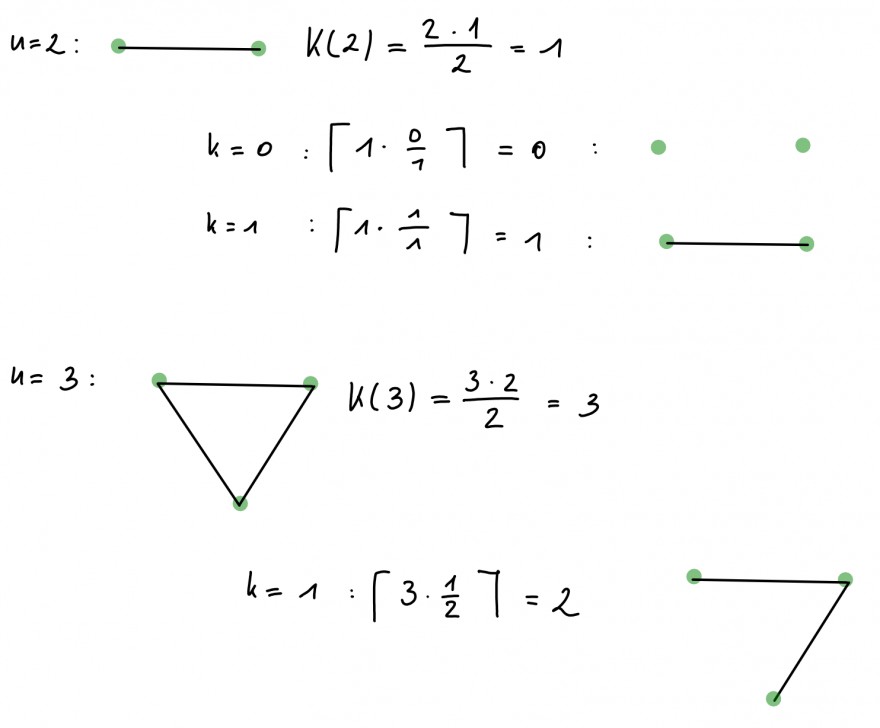Hallo :-)
Der vollständige einfache Graph mit \(n\in \mathbb{N}_{\geq 2}\) Knoten hat genau
\(K(n):=\begin{pmatrix}n\\2\end{pmatrix}=\frac{n(n-1)}{2}\) Kanten.
Jeder Knoten hat zunächst \(n-1\) Kanten.
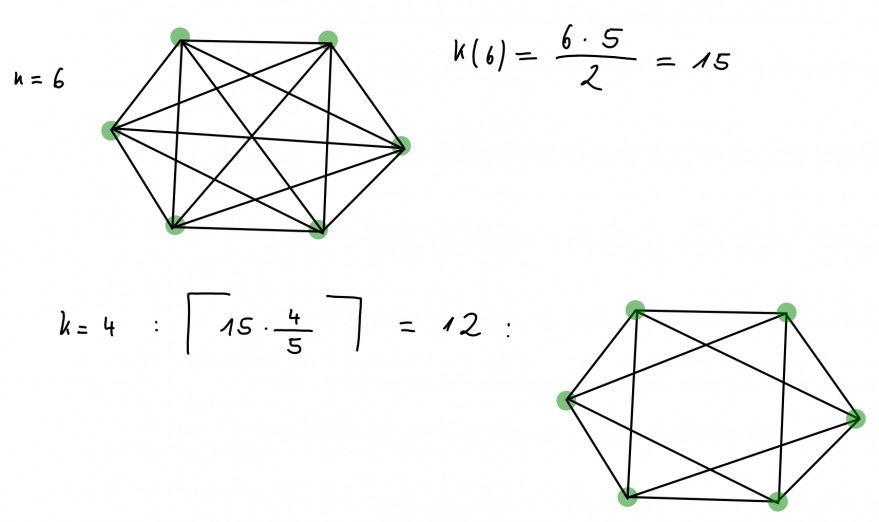
Nun sucht man die Mindestanzahl an benötigten Kanten, sodass jeder der \(n\) Knoten mit mindestens \(k\in \{0,1,2,...,n-2,n-1\}\) in Verbindung steht. Damit hast du folgende Anzahl
\(A(n,k):=\lceil{K(n)\cdot \frac{k}{n-1}\rceil}=\lceil{\frac{n(n-1)}{2}\cdot \frac{k}{n-1}\rceil}=\lceil{\frac{n\cdot k}{2}\rceil}\).
Hier mal ein paar kleinere Beispiele: