Aufgabe:
… Dreifachintegral, Volumen eines Körpers berechnen
Problem/Ansatz:
Habe das im kartesichen Koordinaten und Zylinderkkordinaten probiert zu rechnen aber es kommt nicht das richtige raus. Im kartesischen löst sich alles am Ende auf und kommt 0 raus. In Zylinderkoordinaten bleiben am Ende zu viele unbekannte (y und x) noch stehen. Die Lösung ist 216π.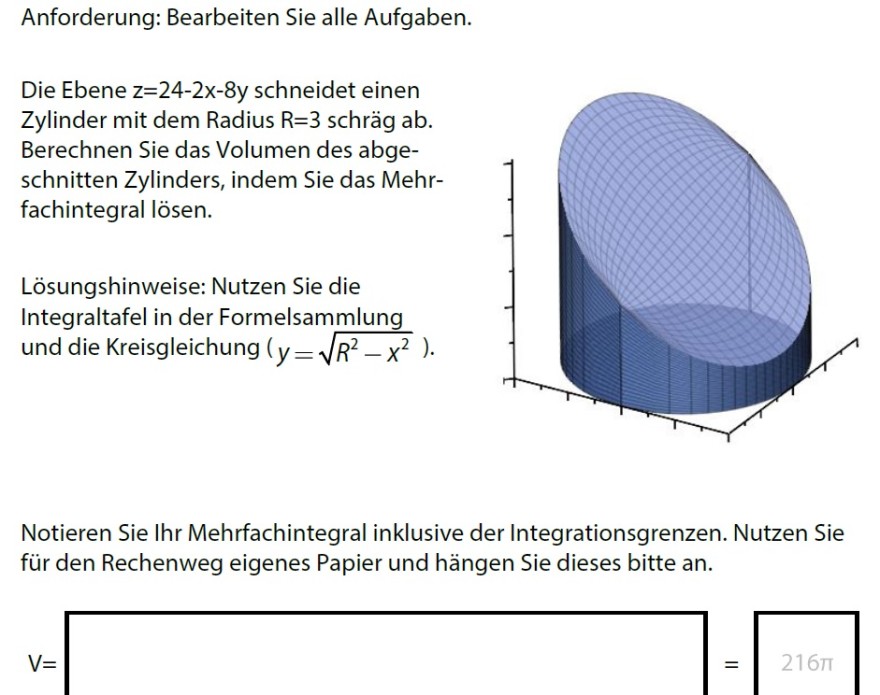
Text erkannt:
Anforderung: Bearbeiten Sie alle Aufgaben.
Die Ebene \( z=24-2 x \)-8y schneidet einen
Zylinder mit dem Radius \( \mathrm{R}=3 \) schräg \( \mathrm{ab} \).
Berechnen Sie das Volumen des abge-
schnitten Zylinders, indem Sie das Mehrfachintegral lösen.
Lösungshinweise: Nutzen Sie die
Integraltafel in der Formelsammlung und die Kreisgleichung \( \left(y=\sqrt{R^{2}-x^{2}}\right) \).
Notieren Sie Ihr Mehrfachintegral inklusive der Integrationsgrenzen. Nutzen Sie für den Rechenweg eigenes Papier und hängen Sie dieses bitte an.
\( \mathrm{V}= \)
Bitte um Hilfe, bin schon 2 Tage am Verzweifeln. Danke EUCH !